12: Difference in Differences (DID)

Impact (Program) Evaluation

---

Impact Evaluation

• What is it?
• Gold standard
• Natural (Quasi) Experiment

Definition

Impact (program) evaluation is a field of econometrics that focuses on estimating the impact of a program or event.

Examples

• Groundwater use limit in Nebraska \(\Rightarrow\) water use
• Technology adoption (soil moisture sensor) \(\Rightarrow\) water use
• Crop insurance \(\Rightarrow\) input use
• Job training program \(\Rightarrow\) productivty
• Food Stamp \(\Rightarrow\) health, education, etc

Key challenge

Most of the programs you are interested in evaluating are not randomized.

\(\;\;\;\;\;\;\;\;\;\downarrow\)

Endogeneity problem arising from self-selection into the program.

Gold Standard

• The best (if feasible) way to tackle the problem of selection bias in impact evaluation is randomized experiment, where who gets treated or not is determined randomly (you design a program or experiment and randomize treatment-control assignment)

• This ensures that the treatment status (dummy variable indicating treated or not) is not correlated with the error term

Example

\(y \;\;(\mbox{income}) = \beta_0 + \beta_1 program \;\;(\mbox{financial aid}) + u\)

, where \(E[u|program]=0\) (the program is not correlated with the error term). OLS is just fine.

Problem

Many of the programs are simply not possible to randomize because of financial and/or ethical reasons.

\(\downarrow\)

We need to use data from an event that happened outside our control.

Definition

An event or policy change (often a change in government policy) that happens outside of the control of investigators, which changes the environment in which agents (individuals, families, firms, or cities) operate.

Challenges

The program is most likely correlated with the error term.

Assessment of various approaches

• Lecture objectives
• Example program
• Data
• Various approaches to evaluate

• Discuss different ways of estimating the impact of a program including the difference in differences (DID) method.

• Understand the strength and weakness of these methods

Incinerator Construction

• rumored about the incinerator being built in North Andover, Massachusetts, began in 1978

• construction started in 1981

Data collected

Housing prices in 1978 and 1981, and other variables (we observations before and after the incinerator construction)

Approach 1

Cross-sectional comparison of houses that are close to (treated) and far away from (control) to the incinerator after the incinerator was built (data in 1981)

Approach 2

Comparison of the houses that are close to the incinerator before (control) and after (treated) the incinerator was built (data in 1978 and 1981)

Approach 3

Comparison of differences (close by v.s. far away) in differences (before-after) of house prices (this method will become clearer later)

Approach 1

• Estimation strategy
• Interpretation
• Estimate
• Take a look at 1978
• Visualization
• Understanding the approach

Run regression on the following model using the 1981 data (cross-sectional data)

\(rprice = \gamma_0 + \gamma_1 nearinc + u\)

• \(rprice\): house price in real terms (inflation-corrected)

• \(nearinc\): 1 if the house is near the incinerator, and 0 otherwise

Question

Is nearinc endogenous?

Model

\(rprice = \gamma_0 + \gamma_1 nearinc + u\)

Question

What does \(\gamma_1\) measure?

Answer

\(\gamma_1\) : the difference between the mean house price of houses nearby the incinerator and the rest (not nearby) in 1981

\[\begin{align*} & E[rprice | nearinc = 1, year = 1981] = \gamma_0 + \gamma_1 \\ & E[rprice | nearinc = 0, year = 1981] = \gamma_0 \end{align*}\]

This means:

\[\begin{align*} \gamma_1 = E[rprice | nearinc = 1, year = 1981] - E[rprice | nearinc = 0, year = 1981] \end{align*}\]

Question Is this reliable?

Run regression on the following model using the 1978 data (cross-sectional data).

\[\begin{align*} rpice = \gamma_0 + \gamma_1 nearinc + u \end{align*}\]

\(\gamma_1\) represents the difference between the mean house price of houses nearby the incinerator and the rest (not nearby) before the incinerator was built.

Critical

The price of houses nearby the incinerator were already lower than those houses that are not nearby before the incinerator was built.

treated	before	after
nearinc = 0	\(\gamma_0\)	\(\gamma_0 + \alpha_0 + 0\)
nearinc = 1	\(\gamma_1\)	\(\gamma_1 + \alpha_1 + \beta \)

• \(\gamma_j\) is the average house price of those that are \(nearinc=j\) in 1978 (before)

• \(\alpha_j\) is any macro shocks other than the incinerator event that happened between the before and after period to the houses that are \(nearinc=j\)

• \(\beta\) is the true causal impact of the incinerator placement

What did we estimate with Approach 1?

\[\begin{align*} & E[rprice|nearinc = 1, year = 1981] \\ & \;\; - E[rprice|nearinc = 0, year = 1981] \\ & \;\;= (\gamma_1 + \alpha_1 + \beta) - (\gamma_0 + \alpha_0 + 0) \\ & \;\;= (\gamma_1 - \gamma_0)+ (\alpha_1 - \alpha_0) + \beta \end{align*}\]

• \(\gamma_1 - \gamma_0\): pre-existing differences in house price before the incinerator was built

• \(\alpha_1 - \alpha_0\): differences in the trends in housing price between the two groups

Question

So, when Approach 1 gives us unbiased estimation of the impact of the incinerator?

Answer

• \(\gamma_1 = \gamma_0\): the average house price between the two groups are the same before the incinerator was built

• \(\alpha_1 - \alpha_0\): the two groups experienced the same house price trend from 1978 to 1981

Approach 2

• Estimation strategy
• Interpretation
• Estimate
• Understanding the approach

Estimation strategy

Comparison of the houses that are close to the incinerator before (control) and after (treated) the incinerator was built (data in 1978 and 1981)

Data

Restrict the data to the houses that are nearby the incinerator.

Model

\(rpice = \beta_0 + \beta_1 y81 + u\)

• \(rprice\): house price in real terms (inflation-corrected)

• \(y81\): 1 if the house is near the incinerator, and 0 otherwise

Model

\(rpice = \beta_0 + \beta_1 y81 + u\)

Question

What does \(\beta_1\) measure?

Answer

\(\beta_1\): the difference in the mean house price of houses nearby the incinerator before and after the incinerator was built

\[\begin{align*} & E[rprice | nearinc = 1, year = 1978] = \beta_0 \\ & E[rprice | nearinc = 1, year = 1981] = \beta_0 + \beta_1 \end{align*}\]

This means:

\[\begin{align*} \beta_1 = E[rprice | nearinc = 1, year = 1981] - E[rprice | nearinc = 1, year = 1978] \end{align*}\]

The incinerator increased the average house price (not statistically significant)!

treated	before	after
nearinc = 0	\(\gamma_0\)	\(\gamma_0 + \alpha_0 + 0\)
nearinc = 1	\(\gamma_1\)	\(\gamma_1 + \alpha_1 + \beta \)

• \(\gamma_j\) is the average house price of those that are \(nearinc=j\) in 1978 (before)

• \(\alpha_j\) is any macro shocks other than the incinerator event that happened between the before and after period to the houses that are \(nearinc=j\)

• \(\beta\) is the true causal impact of the incinerator placement

What did we estimate with Approach 2?

\[\begin{align*} & E[rprice|nearinc = 1, year = 1981] \\ & \;\;- E[rprice|nearinc = 1, year = 1978] \\ & \;\;= (\gamma_1 + \alpha_1 + \beta) - \gamma_1 \\ & \;\;= \alpha_1 + \beta \end{align*}\]

Question

So, when Approach 2 gives us unbiased estimation of the impact of the incinerator?

Answer

\(\alpha_1 = 0\): no trend in house price for the houses near the incinerator (Nothing else significant other than the incinerator happened between 1978 and 1981.)

Approach 3

• Estimation strategy
• DID
• Estimate
• Understanding the approach
• Parallel trend

Estimation strategy (difference-in-differences or DID)

Compare of differences (close by v.s. far away) in differences (before-after) of house prices (this method will become clearer later)

• Find the difference in the price of the houses close to the incinerator before and after the incinerator was built

• Find the difference in the price of the houses far away from the incinerator before and after the incinerator was built

• Find the difference in the differences

Data

All the observations (1978 and 1981, treated and non-treated)

Model

\(rpice = \beta_0 + \beta_1 y81 + \beta_2 nearinc + \beta_3 nearinc \times y81 + u\)

• \(\beta_3\): the difference in differences estimate of the impact of the incinerator

Let’s confirm \(\beta_3\) indeed represents the difference in the differences.

Model

\(rpice = \beta_0 + \beta_1 y81 + \beta_2 nearinc + \beta_3 nearinc \times y81 + u\)

Expected house price

• \(E[rprice|year=1981, nearinc = 0] = \beta_0 + \beta_1\)

• \(E[rprice|year=1981, nearinc = 1] = \beta_0 + \beta_1 + \beta_2 + \beta_3\)

• \(E[rprice|year=1978, nearinc = 0] = \beta_0\)

• \(E[rprice|year=1978, nearinc = 1] = \beta_0 + \beta_2\)

Differences

\(E[rprice|year=1981, nearinc = 1] - E[rprice|year=1978, nearinc = 1]\)

\(= (\beta_0 + \beta_1 + \beta_2 + \beta_3) - (\beta_0 + \beta_2)\) \(= \beta_1 + \beta_3\)

\(E[rprice|year=1981, nearinc = 0] - E[rprice|year=1978, nearinc = 0]\)

\(= (\beta_0 + \beta_1) - \beta_0\) \(= \beta_1\)

Difference in the differences

\((\beta_1 + \beta_3) - \beta_1 = \beta_3\)

The incinerator decreased the average house price (not statistically significant).

treated	before	after
nearinc = 0	\(\gamma_0\)	\(\gamma_0 + \alpha_0 + 0\)
nearinc = 1	\(\gamma_1\)	\(\gamma_1 + \alpha_1 + \beta \)

What did we estimate with Approach 3?

\[\begin{align*} & E[rprice|nearinc = 1, year = 1981] \;\; - E[rprice|nearinc = 1, year = 1978] \;\; = (\gamma_1 + \alpha_1 + \beta) - \gamma_1 = \alpha_1 + \beta \\ & E[rprice|nearinc = 0, year = 1981] \;\; - E[rprice|nearinc = 0, year = 1978] \;\; = (\gamma_0 + \alpha_0) - \gamma_0 = \alpha_0 \end{align*}\] \[\begin{align*} \downarrow \end{align*}\] \[\begin{align*} \widehat{\beta}_{DID} = \alpha_1 - \alpha_0 + \beta \end{align*}\]

Question

So, when Approach 3 gives us unbiased estimation of the impact of the incinerator?

Answer

• \(\alpha_1 = \alpha_0\): the two groups experienced the same trend in house price from 1978 to 1981

• Unlike Approach 1, the pre-existing difference between the two group is not a problem as it gets canceled out

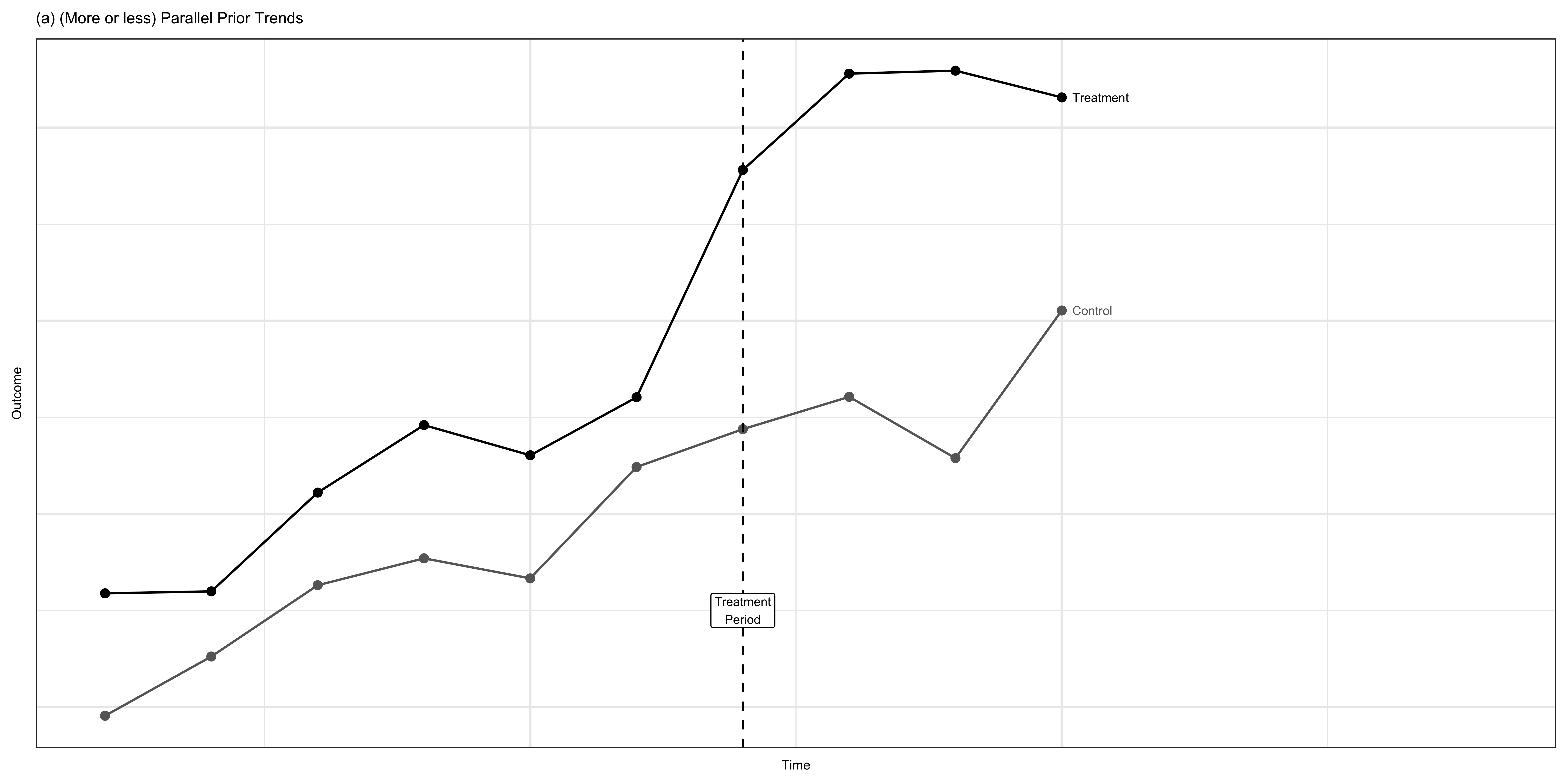
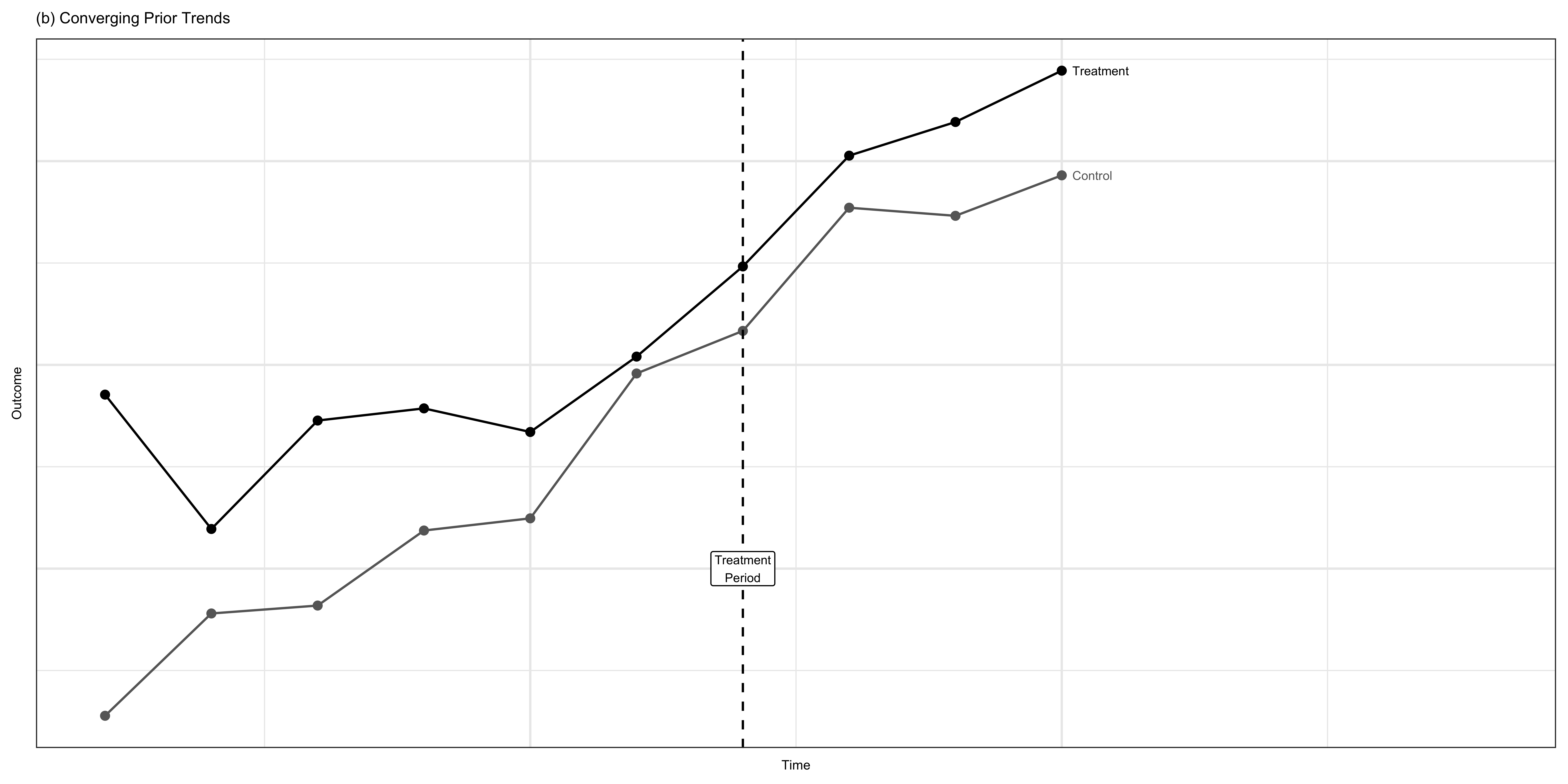
Key condition (common/parallel trend assumption)

\(\alpha_1 = \alpha_0\): the two groups experienced the same trend in house price from 1978 to 1981

Common/parallel trend assumption in general

If no treatment had occurred, the difference between the treated group and the untreated group would have stayed the same in the post-treatment period as it was in the pre-treatment period.

Important

This condition/assumption is NOT testable because you never observe what would the treament group be like if it were not for the treatment (we will discuss this further)

Summary of the approaches

Approaches

Approach 1: \((\gamma_1 - \gamma_0)+ (\alpha_1 - \alpha_0) + \beta\)

Approach 2: \(\alpha_1 + \beta\)

Approach 3: \(\alpha_1 - \alpha_0 + \beta\)

Important

• None of these approaches are perfect.

• It is hard to sell Approaches 1 and 2

• Approach 3 (DID) is preferred over Approaches 1 and 2

• But, Approach 3 is not certainly perfect and could definitely have a larger bias than Approaches 1 and 2

e.g., \(\alpha_1 = 5\) and \(\alpha_0 = - 5\)

DID: Another Example

• Context
• Control/treatment
• DID estimate

Cholera

• Back in mid 1800s’, Cholera was believed to spread via air
• John Snow believe it was actually through fecally-contaminated water

Setting

• London’s water needs were served by a number of competing companies, who got their water intake from different parts of the Thames river.

• Water taken in from the parts of the Thames that were downstream of London contained everything that Londoners dumped in the river, including plenty of fecal matter from people infected with cholera.

Natural Experiment

• Between those two periods of 1849 and 1854, a policy was enacted: the Lambeth Company was required by an Act of Parliament to move their water intake upstream of London.

Treatment

• Switch of where water is taken (downstream to upstream)

Before and After

• “before” (1849): Lambeth took water downstream
• “after” (1854): Lambeth took water upstream

Control and Treatment Groups

• Control group: those who were not served by Lambeth
• Treatment group: those who were served by Lambeth

Data

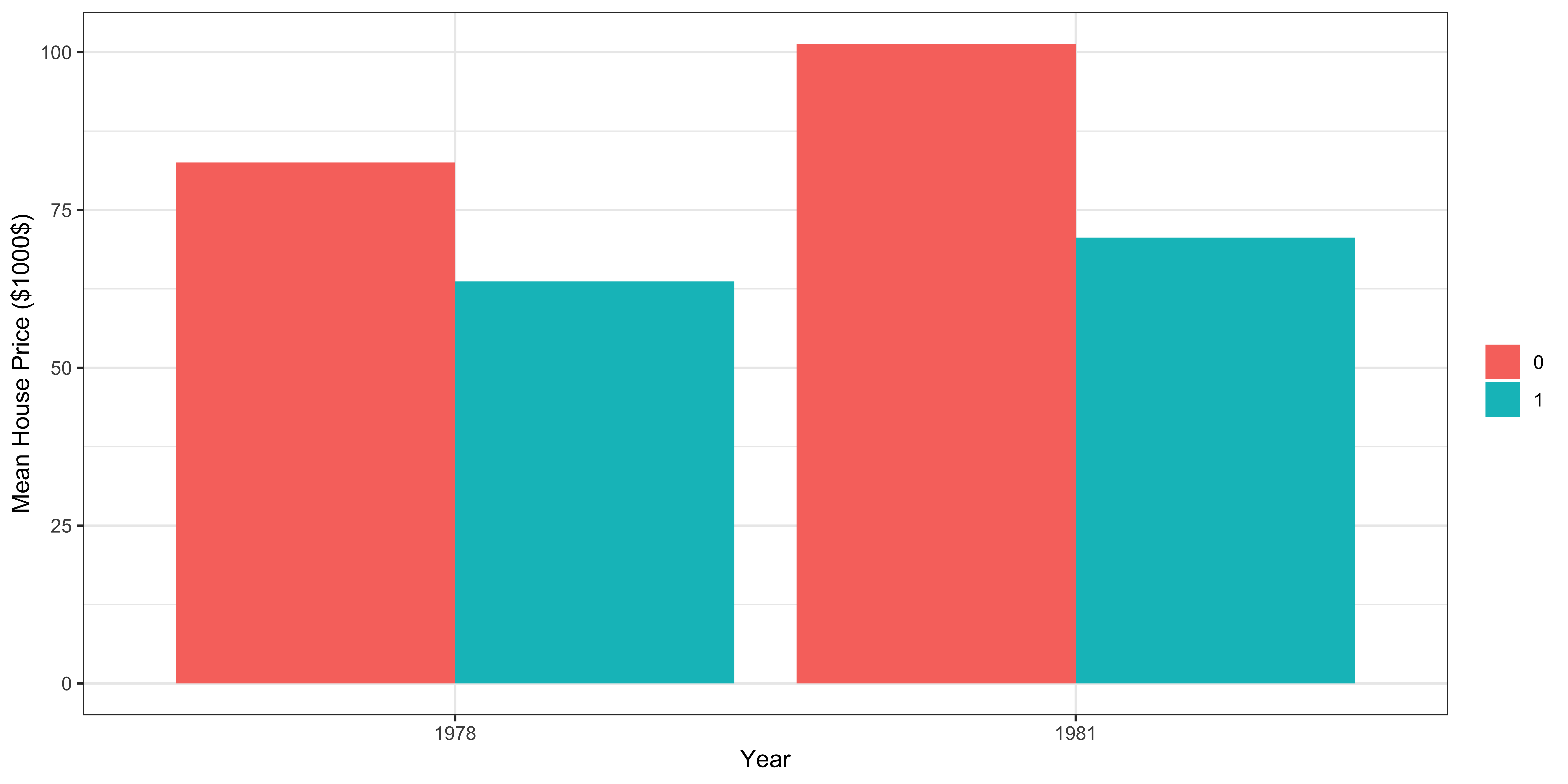
Supplier	1849	1854
Non-Lambeth only	134.9	130.1
Lambeth + Others	146.6	84.9

DID estimate

Estimate treatment effect is:

(84.9 - 130.1) - (146.6 - 134.9) = -56.9

DID implementation using R

• Data
• Control and treated
• Prepare variables for DID
• Estimation
• Individual FEs
• Year FEs

Well-level groundwater use data in Kansas

(
  lema_data <- readRDS("LEMA_data.rds")
)

        site  year    af_used in_LEMA    pr       et0       awc bulkdensity
       <int> <num>      <num>   <num> <num>     <num>     <num>       <num>
    1:   160  1991 195.328540       1 401.9 1047.3311 0.1859333    1.359156
    2:   160  1992  62.390479       1 463.9  904.0815 0.1859333    1.359156
    3:   160  1993  40.214699       1 615.6  842.7572 0.1859333    1.359156
    4:   160  1994 155.113840       1 405.5 1028.4635 0.1859333    1.359156
    5:   160  1995 103.093132       1 488.5  890.5116 0.1859333    1.359156
   ---                                                                     
34121: 82261  2019   5.277566       0 598.4  961.0884 0.2078054    1.383747
34122: 82288  2018   0.007672       0 425.7 1069.7815 0.1823573    1.269078
34123: 82538  2017 195.000000       0 563.2 1027.4662 0.2063358    1.287400
34124: 82538  2018 158.000000       0 554.7 1092.2203 0.2063358    1.287400
34125: 82538  2019 136.000000       0 544.8 1011.2639 0.2063358    1.287400

Main variables

• site: well
• af_used: groundwater used (dependent variable)
• in_LEMA: whether located inside the LEMA region or not
• year: year

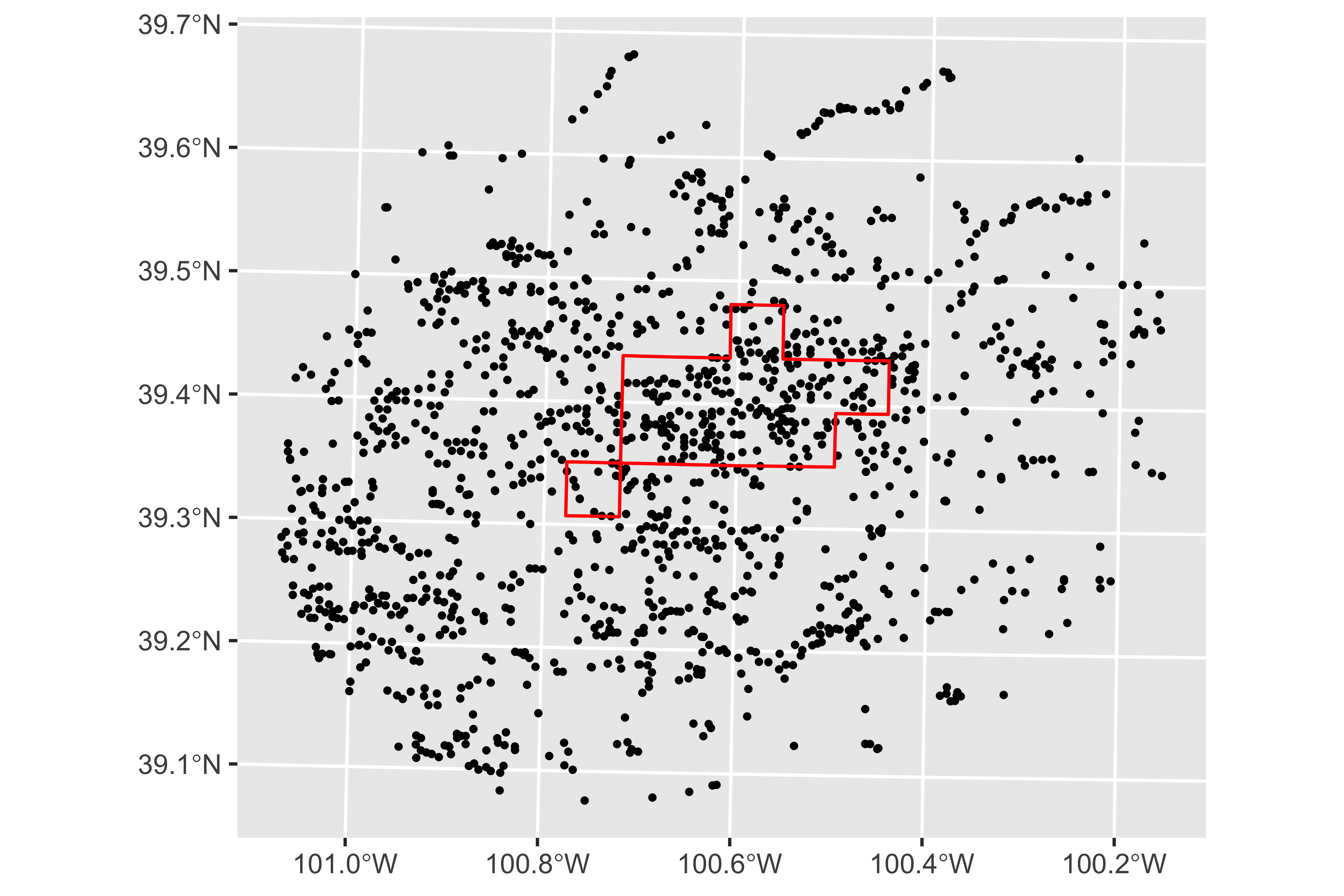
Control and Treatment Units

• (to be) treated: wells inside the red boundary (LEMA)
• control: wells outside the red boundary (LEMA)

Before and After

Effective 2013, wells located inside the LEMA can pump groundwater up to a certian amount

• before: ~ 2012
• after: 2013 ~

Data transformation:

before or after

lema_data <- mutate(lema_data, before_after = ifelse(year >= 2013, 1, 0))

Take a look at the one of the wells:

lema_data %>%
  dplyr::select(site, year, before_after) %>%
  dplyr::filter(site == 160, year > 2000)

     site  year before_after
    <int> <num>        <num>
 1:   160  2001            0
 2:   160  2002            0
 3:   160  2003            0
 4:   160  2004            0
 5:   160  2005            0
 6:   160  2006            0
 7:   160  2007            0
 8:   160  2008            0
 9:   160  2009            0
10:   160  2010            0
11:   160  2011            0
12:   160  2012            0
13:   160  2013            1
14:   160  2014            1
15:   160  2015            1
16:   160  2016            1
17:   160  2017            1
18:   160  2019            1

(to be) treated or not

Whether wells are (to be) treated or not is already there in this dataset, represented by in_LEMA

DID estimating equation (in general)

\[ \begin{aligned} y_{i,t} = \alpha_0 + \beta_1 before\_after_t + \beta_2 treated\_or\_not_i + \beta_3 before\_after_t \times treated\_or\_not_i + X_{i,t}\gamma + v_{i,t} \end{aligned} \]

The variable of interest is \(\beta_3\), which measures the impact of the treatment.

R code

fixest::feols(
  af_used ~ before_after + in_LEMA + I(before_after * in_LEMA) + pr + et0,
  cluster = ~site,
  data = lema_data
)

OLS estimation, Dep. Var.: af_used
Observations: 34,125 
Standard-errors: Clustered (site) 
                            Estimate Std. Error   t value  Pr(>|t|)    
(Intercept)               185.829056   7.153231  25.97834 < 2.2e-16 ***
before_after               -9.034901   1.034500  -8.73359 < 2.2e-16 ***
in_LEMA                    30.001586   3.224780   9.30345 < 2.2e-16 ***
I(before_after * in_LEMA) -34.762264   2.097251 -16.57516 < 2.2e-16 ***
pr                         -0.187841   0.005100 -36.83260 < 2.2e-16 ***
et0                         0.013708   0.005033   2.72326 0.0065454 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 71.4   Adj. R2: 0.10752

DID does NOT require panel data. Two periods of cross-setional data are sufficient. But, if you have panel data, you can certainly include individual fixed effects, which would certainly help to control for time-invariant characteristics (both observed and unobserved)

fixest::feols(
  af_used ~ before_after + in_LEMA + I(before_after * in_LEMA) + pr + et0 | site,
  cluster = ~site,
  data = lema_data
)

OLS estimation, Dep. Var.: af_used
Observations: 34,125 
Fixed-effects: site: 1,383
Standard-errors: Clustered (site) 
                            Estimate Std. Error   t value   Pr(>|t|)    
before_after               -8.748317   0.837889 -10.44090  < 2.2e-16 ***
I(before_after * in_LEMA) -36.550589   1.961441 -18.63456  < 2.2e-16 ***
pr                         -0.185034   0.004263 -43.40657  < 2.2e-16 ***
et0                         0.019343   0.003955   4.89076 1.1221e-06 ***
... 1 variable was removed because of collinearity (in_LEMA)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 43.6     Adj. R2: 0.652695
             Within R2: 0.226595

Notice that in_LEMA was dropped due to perfect collinearity (this is not a problem). in_LEMA is effectively controlled for by including individual fixed effects.

If you have multiple years of observations in the before and after periods, you can (and should) include year fixed effects.

fixest::feols(
  af_used ~ before_after + in_LEMA + I(before_after * in_LEMA) + pr + et0 | site + year,
  cluster = ~site,
  data = lema_data
)

OLS estimation, Dep. Var.: af_used
Observations: 34,125 
Fixed-effects: site: 1,383,  year: 29
Standard-errors: Clustered (site) 
                            Estimate Std. Error   t value  Pr(>|t|)    
I(before_after * in_LEMA) -37.149761   1.961915 -18.93546 < 2.2e-16 ***
pr                         -0.114725   0.007728 -14.84493 < 2.2e-16 ***
et0                         0.052997   0.030668   1.72807  0.084198 .  
... 2 variables were removed because of collinearity (before_after and in_LEMA)
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 40.7     Adj. R2: 0.698229
             Within R2: 0.025545

Notice that before_after was dropped due to perfect collinearity (this is not a problem). before_after is effectively controlled for by including year fixed effects. Indeed, year fixed effects provide a tighter controls on annual macro shocks.

How to argue your DID is reliable

• Prallel trend condition
• Examples of trends
• the LEMA case
• Placebo tests
• 2000
• 1995
• What if

Important

Selecting the right control group is important in DID. If the following conditions are satisfied, it is more plausible that the control and treatment groups would have had the same macro shock \((\alpha_1 = \alpha_0)\) if it were not for the treatment.

• There were no events that could significantly affect the dependent variable of the control group between the “before” and “after” period
• The two groups are generally similar so other factors do not drive the differences between them
• They had similar trajectories of the dependent variable prior to the treatment (possible if you have more than one years of data prior to the treatment)
  • this does NOT guarantee that the their trends after the treatment are similar

To do

• Show the trajectory of the dependent variable
• Run placebo tests

• Example 1
• Example 2

So, how about our example?

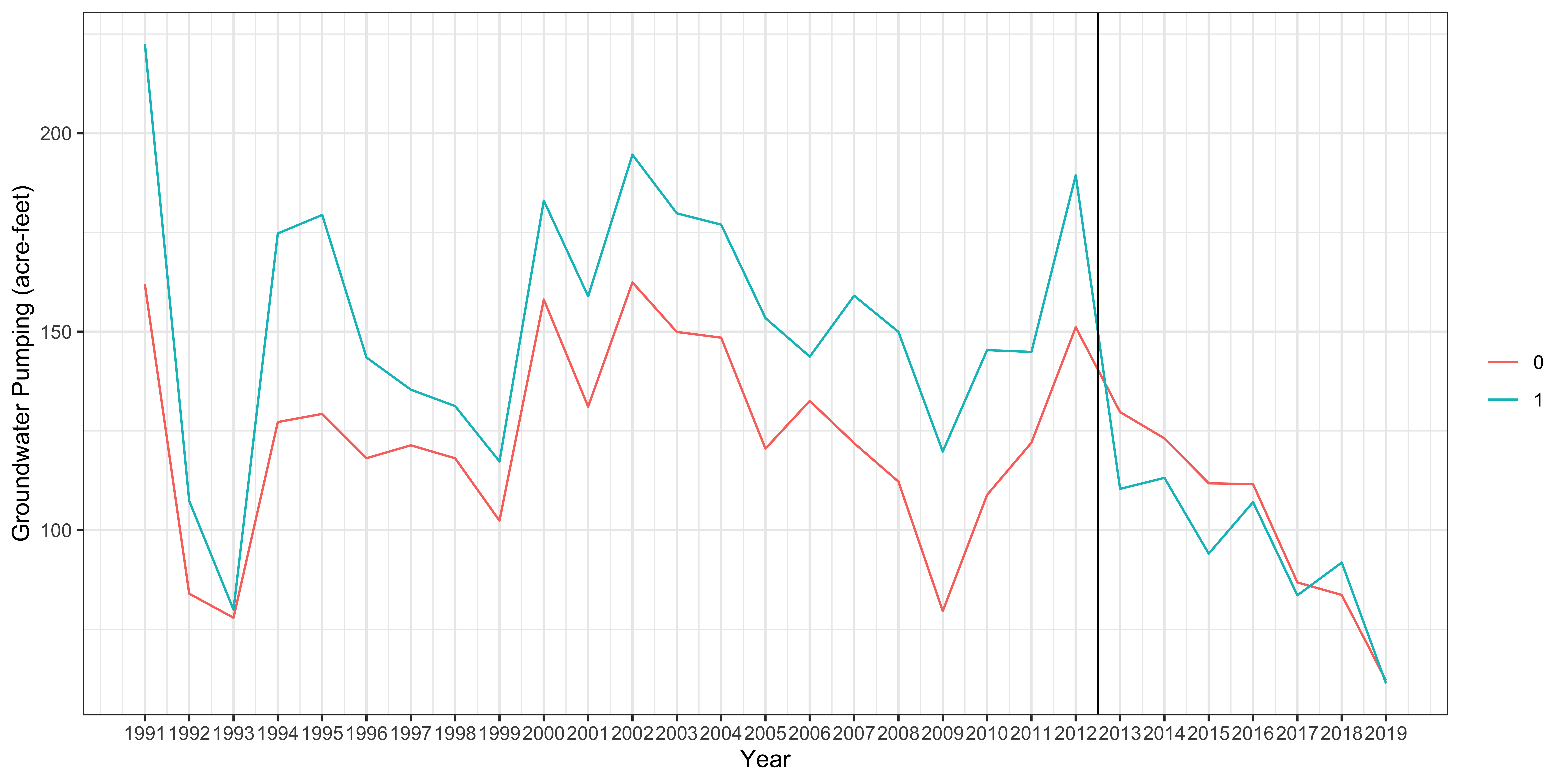
Not too bad. We might want to consider starting from 1993.

Placebo tests: idea

• Look at only the pre-treatment periods
• Pretend that a treatment happend sometime in the middle of the pre-treatment period to the actual treatment group
• Estimate the impact of the fake treatment
• Check if the estimated impact is stastitically insignificantly different from 0
• If statistically significant, that would mean there is likley to be something wrong with the parallel trende assumption

Note

Statistically insignificant estimated impacts of fake treatments bolster your claim about parallel trend assumption. But, it still does NOT guarantee the assumption is valid. Remember, the assumption is not testable.

Create a fake treament for the wells inside LEMA in 2000.

pre_lema_data <-
  filter(lema_data, year <= 2012 & year >= 1993) %>%
  #* pretend that a treatment happend in 2000
  mutate(after_2000 = ifelse(year >= 2000, 1, 0))

Estimate the impact of the fake treatment variable:

(
  fixest::feols(
    af_used ~ I(after_2000 * in_LEMA) + pr + et0 | site + year,
    cluster = ~site,
    data = pre_lema_data
  )
)

OLS estimation, Dep. Var.: af_used
Observations: 23,509 
Fixed-effects: site: 1,358,  year: 20
Standard-errors: Clustered (site) 
                         Estimate Std. Error    t value  Pr(>|t|)    
I(after_2000 * in_LEMA)  1.988322   2.588713   0.768073   0.44258    
pr                      -0.214327   0.017302 -12.387431 < 2.2e-16 ***
et0                     -0.005044   0.046476  -0.108533   0.91359    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 39.5     Adj. R2: 0.71128 
             Within R2: 0.008306

Create a fake treament for the wells inside LEMA in 1995.

pre_lema_data <-
  filter(lema_data, year <= 2012 & year >= 1993) %>%
  #* pretend that a treatment happend in 1995
  mutate(after_1995 = ifelse(year >= 1995, 1, 0))

Estimate the impact of the fake treatment variable:

(
  fixest::feols(
    af_used ~ I(after_1995 * in_LEMA) + pr + et0 | site + year,
    cluster = ~site,
    data = pre_lema_data
  )
)

OLS estimation, Dep. Var.: af_used
Observations: 23,509 
Fixed-effects: site: 1,358,  year: 20
Standard-errors: Clustered (site) 
                         Estimate Std. Error    t value  Pr(>|t|)    
I(after_1995 * in_LEMA) -2.353117   2.910581  -0.808470   0.41896    
pr                      -0.214146   0.017320 -12.363797 < 2.2e-16 ***
et0                      0.007087   0.047450   0.149355   0.88130    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 39.5     Adj. R2: 0.711271
             Within R2: 0.008276

You can try more years as the starting year of a fake treatment and see what happens.

What if your data spans from 1991 to 2000 with a treatment occuring at 1993?

pre_lema_data <-
  filter(lema_data, year <= 2000) %>%
  #* pretend that a treatment happend in 1993
  mutate(after_1993 = ifelse(year >= 1993, 1, 0))

did_res_placebo <-
  feols(
    af_used ~ I(after_1993 * in_LEMA) + pr + et0 | site + year,
    cluster = ~site,
    data = pre_lema_data
  )

Let’s look at the regression results:

msummary(
  did_res_placebo,
  gof_omit = "IC|Log|Adj|F|Pseudo|Within",
  output = "flextable",
  star = TRUE
) %>%
  fontsize(size = 9, part = "all") %>%
  color(i = 1, j = 2, color = "red") %>%
  autofit()

	(1)
I(after_1993 * in_LEMA)	-16.386***
	(3.900)
pr	-0.121***
	(0.026)
et0	0.114+
	(0.065)
Num.Obs.	11320
R2	0.715
RMSE	40.96
Std.Errors	by: site
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001

• So, this tells you that if it was a real treatment of which you want to understand the impact, then you would have suffered significant bias.
• This clearly indicates that DID is by no means perfect and indeed can be very dangerous