11: Dealing with Endogeneity: Instrumental Variables
Instrumental Variable (IV) Approach
Transcript
Let us begin by being precise about the problem IV is meant to solve. The equation on screen says that the expected value of the error, conditional on all of the explanatory variables from x one through x k, is not zero. In other words, once you know the regressors, you can systematically predict something about the error. That violates the zero conditional mean assumption that gives OLS a causal interpretation.
The next definition focuses on one regressor. If x k is correlated with the error term, we call x k endogenous. The error contains every unobserved determinant of the outcome, so this correlation means that changes in x k come bundled with changes in something omitted from the regression. OLS cannot tell which part of the resulting outcome difference came from x k itself.
The four bullets list common routes to that failure. With an omitted variable, a factor left in the error affects both the regressor and the outcome. With selection, the observations or treatment status enter the sample through a process related to unobserved outcomes. With reverse causality, the outcome also helps determine the supposed cause. With measurement error, the observed regressor differs from the true regressor, and that discrepancy becomes part of the regression error. These mechanisms are different, but each can create correlation between a regressor and the structural error.
Instrumental variables do not somehow make the original regressor exogenous. Instead, IV looks for a separate source of variation that moves the endogenous regressor but is unrelated to the outcome error. We will use only that isolated variation to estimate the causal effect. The next tab draws the endogeneity problem as a causal diagram, which will make the source of the OLS failure visible.
Endogeneity
E[u\mid x_1,\dots,x_k]\ne0
The zero-conditional-mean assumption fails: the error term is systematically related to at least one explanatory variable.
Endogenous independent variable
If an explanatory variable x_k is correlated with the error term, we call x_k an endogenous explanatory variable.
- Omitted variable
- Selection
- Reverse causality
- Measurement error
Transcript
Here is the running example in a causal diagram. The two bullets above the figure identify the target: education is the explanatory variable whose causal effect we want, and income is the outcome. In the diagram, the arrow from Education to Income is therefore the causal relationship we would like to estimate.
Now trace every other arrow. Experience points to Income because labor-market experience can affect earnings, and it is an observed variable that we can include as a control. The box labeled Error contains ability plus other determinants that we have not observed or have not included separately. It points to Income because ability and those other factors affect earnings. Crucially, it also points to Education because ability, preferences, family circumstances, or similar omitted factors can influence how much schooling a person obtains.
That pair of arrows creates the backdoor path Education, Error, Income. People with different education levels will tend to differ in the omitted factors even before education has any causal effect. A regression of income on education and experience would then use two kinds of education variation at once: variation that might causally change income, and variation associated with ability and the other contents of the error. Controlling for experience blocks the path through experience if the specification is adequate, but it does not block the path through the unobserved Error node. Consequently, the education coefficient generally combines the causal effect with omitted-variable confounding.
The code shown above the figure is only how the diagram was generated. The substantive lesson is the arrow pattern. On the next tab we add a new variable, Z, and ask what arrows it may and may not have if it is to solve this problem.
You want to estimate the causal impact of education on income.
- Variable of interest: Education
- Dependent variable: Income
Causal diagram
Transcript
Now look at the new node Z on the left. We want Z to create a particular chain: Z changes Education, and Education in turn changes Income. The arrow from Z to Education represents relevance. In words, Z must predict education even after we control for the other exogenous variables, such as experience. If Z does not move education, it gives us no new education variation with which to learn the education effect.
The absence of arrows is just as important as the arrow we see. Exclusion means there is no direct arrow from Z to Income. After holding education and the included controls fixed, Z must not change income through any other channel. Exogeneity means Z is uncorrelated with the structural error, including ability. In a fuller diagram, there must be no unblocked common cause that makes Z vary with unobserved determinants of income.
If all three ideas hold, we can compare the part of education that changes because Z changes. That instrument-induced education variation travels to income through the causal arrow we care about, while avoiding the backdoor path through ability. Notice that experience still points to income, so it remains an included control. The instrument is not a substitute for correctly specifying the exogenous controls.
This picture also shows why a good prediction of education is necessary but insufficient. A variable could have a very strong Z-to-Education arrow and still be invalid if it directly affects income or shares an unobserved cause with income. Relevance is an empirical first-stage question. Exclusion and exogeneity are causal design claims. Keep those three concepts separate as we translate the diagram into two-stage least squares on the next tab.
We want to find a variable like Z in the diagram below:
- Relevance: Z predicts education after controlling for the other exogenous variables.
- Exclusion: Z affects income only through education; it has no direct effect on income.
- Exogeneity: Z is uncorrelated with unobserved determinants of income in the structural error, including ability.
Transcript
The model at the top is the structural outcome equation. Y is the outcome. Beta zero is the intercept. Beta one is the causal coefficient on x one, the variable of interest. Beta two is the coefficient on x two, an included control. U collects all unobserved determinants of y.
The first bullet says x one is endogenous. The conditional expectation of u given x one and x two is not zero, and typically x one and u have nonzero covariance. That is why regressing y directly on x one and x two does not generally identify beta one. The second bullet says x two is exogenous: conditioning on x two does not predict the error, and its covariance with u is zero. We therefore keep x two in the outcome equation as an ordinary included control.
The blue phrase introduces one or more instrumental variables, collected in Z. They are excluded instruments because they help explain x one in the first stage but do not appear as separate causes in the structural outcome equation. Exclusion is not merely a formatting choice. It is the substantive claim that these variables affect y only through x one, after the included controls are held fixed. They must also be exogenous, meaning unrelated to u.
The first stage projects x one onto Z together with x two. This separates the part of x one that can be predicted by the proposed instruments and exogenous controls from the remaining endogenous variation. The second stage uses that fitted component to estimate beta one. The phrase instrument-induced variation matters: IV is learning from changes in x one generated by Z, not from every observed difference in x one. Depending on the setting and additional assumptions, that can also determine which population or margin the estimate describes. The next two tabs write the two stages explicitly.
The Model
y=\beta_0 + \beta_1 x_1 + \beta_2 x_2 + u
- x_1 is endogenous: E[u\mid x_1,x_2]\ne0 (and typically \operatorname{Cov}(u,x_1)\ne0)
- x_2 is exogenous: E[u\mid x_2]=0 (and \operatorname{Cov}(u,x_2)=0)
Idea (very loosely put)
Find one or more instrumental variables that are excluded from the structural outcome equation but predict the endogenous variable.
Use the instruments Z to isolate variation in x_1 that is unrelated to the structural error.
Use that instrument-induced variation to estimate the causal effect of x_1 on y.
Transcript
Step one is a projection of the endogenous variable onto the full instrument set. In the first displayed equation, x one is the endogenous variable on the left. Alpha zero is the first-stage intercept. Sigma two is the coefficient on x two, the exogenous variable already included in the structural outcome equation. Alpha one and alpha two are the coefficients on the two excluded instruments, z one and z two. The term v is the first-stage error, which is the part of x one that this linear combination does not explain.
Why is x two on the right-hand side? Every exogenous variable included in the outcome equation must also be included in the first-stage projection. We want variation in the instruments after holding that control fixed, and the final two-stage least-squares projection uses both included and excluded instruments. Leaving x two out of the first stage generally changes the fitted values and therefore changes the estimator. It is not the procedure written on this slide.
After estimating the first-stage coefficients, we form the second line. X one hat is the predicted value of x one. Alpha zero hat, sigma two hat, alpha one hat, and alpha two hat are the estimated coefficients from the first equation. For each observation, we multiply its x two, z one, and z two values by the corresponding estimated coefficients and add the estimated intercept. There is no v term in the fitted value because v is precisely the unexplained residual.
The resulting x one hat is not necessarily the causal or error-free value of x one for a person. It is the component of x one lying in the variation spanned by the instruments and included exogenous variables. Relevance requires z one and z two to add predictive power for x one after x two is controlled for. On the next tab we use that fitted component in the structural equation.
Idea
Project the endogenous variable onto the instruments and all included exogenous variables.
Step 1: mathematically
- Regress the endogenous variable x_1 on the excluded instruments Z=\{z_1,z_2\} and every exogenous variable included in the outcome equation (here, x_2).
x_1 = \alpha_0 + \sigma_2 x_2 + \alpha_1 z_1 +\alpha_2 z_2 + v
- Obtain the predicted value of x_1 from this first-stage regression.
\widehat{x}_1 = \widehat{\alpha}_0 + \widehat{\sigma}_2 x_2 + \widehat{\alpha}_1 z_1 + \widehat{\alpha}_2 z_2
Transcript
Step two uses the fitted component produced in step one. In the displayed equation, y is the outcome, beta zero is the structural intercept, beta one is the coefficient of interest, x one hat is the first-stage prediction, beta two multiplies the included exogenous control x two, and epsilon is the disturbance in this conceptual second-stage regression.
The logic is that x one hat retains only the component of x one explained by the instrument set. If the excluded instruments are relevant, excluded from the outcome equation, and exogenous, that component supplies variation in x one that is not associated with the original structural error. Regressing y on x one hat and x two then reproduces the two-stage least-squares slope coefficients.
The red word “not” marks an important implementation warning. If you literally save x one hat and run an ordinary OLS regression in a second command, the coefficient is the 2SLS coefficient when both stages are specified correctly, but the usual OLS standard error is wrong. That calculation treats x one hat as ordinary observed data. It does not use the proper 2SLS residual calculation and therefore does not report the sampling uncertainty for the IV estimator.
Use these two manual stages to understand where the identifying variation comes from. In an actual analysis, use a dedicated IV command that constructs the coefficient and the appropriate variance estimate together. The example in the next set of tabs first performs the manual steps for intuition, then later shows the proper one-call implementation.
Idea
Use the fitted component of x_1 to estimate the structural coefficient \beta_1.
Step 2: Mathematically
Conceptually, regress y on \widehat{x}_1 and x_2:
y= \beta_0 + \beta_1 \widehat{x}_1+ \beta_2 x_2 + \varepsilon
This reproduces the 2SLS coefficient, but a manually run second-stage OLS regression does not report the correct 2SLS standard errors. In practice, estimate both stages with an IV command.
Transcript
Now map the abstract notation into a wage equation. The dependent variable is the natural log of wage. Beta zero is the intercept. Beta one multiplies years of education, and beta two multiplies labor-market experience. Because the outcome is in logs while education is in levels, one additional year of education is associated approximately with one hundred times beta one percent higher wage, with the exact percentage given by one hundred times exponential beta one minus one.
The structural error is labeled v, and the equation on the right decomposes it into beta three times ability plus e. Ability is omitted because it is unobserved, not because it is unimportant. If ability affects wages and is correlated with education, then education is correlated with v and is endogenous. An OLS education coefficient would mix the return to schooling with wage differences associated with ability. Experience is treated as exogenous in this illustration, meaning we assume it is not correlated with the unobserved determinants collected in v after the model is specified.
The two proposed instruments are IQ score and number of siblings. At this point they are only candidates used to demonstrate the calculation. IQ may predict education, but it is plausibly related to ability and may affect productivity directly, threatening exogeneity and exclusion. Siblings may shift schooling through family resources, but family size may also proxy for background factors that affect wages outside schooling. Calling these variables instruments does not make the assumptions true.
For now, focus on mechanics. The next tab regresses education on experience and the two excluded variables to construct predicted education. Later slides return to whether any such variable deserves a causal interpretation as an instrument.
Model
\log(wage)=\beta_0+\beta_1 educ+\beta_2 exper+v, \qquad v=\beta_3 ability+e
- Regress \log(wage) on educ and exper (ability is omitted because it is unobserved).
- v=\beta_3 ability+e is the structural error term.
- educ is considered endogenous (correlated with ability)
- exper is considered exogenous (not correlated with ability)
Instruments (Z)
Suppose you are considering the following candidate instruments for illustration:
- IQ test score (IQ)
- number of siblings (sibs)
Transcript
The first displayed line is the first-stage regression for this example. Education is the dependent variable. Alpha zero is the intercept; alpha one is the coefficient on experience, the included exogenous control; alpha two is the coefficient on IQ; alpha three is the coefficient on siblings; and r is the unexplained part of education. IQ and siblings are the excluded instruments in this illustrative calculation.
The second line replaces every unknown coefficient with its estimate and removes the residual. Education hat is therefore the predicted years of schooling for each observation: alpha zero hat plus alpha one hat times that person’s experience, plus alpha two hat times IQ, plus alpha three hat times siblings. Moving from the first line to the second is just fitting the regression and retaining its systematic component.
Now read the code from top to bottom. The data call loads the wage two data from the wooldridge package. Fixest double-colon fee-ols estimates education on experience plus IQ plus siblings, with the data argument telling the function to find those columns in wage two; the fitted model is stored as first underscore reg. The mutate call then adds a column named education underscore hat. Its values come from first underscore reg, dollar, fitted dot values, so every row receives its own first-stage prediction. Finally, the pipe sends the updated data to relocate, which moves education underscore hat to the first column for visibility, and then to head, which prints the first six rows.
In those rows, predicted education is about 13.26, 14.81, 14.15, 12.80, 10.74, and 14.09 years. Compare those with the observed education values later in each row. They are not generally equal, and predicted years need not be whole numbers. Education hat is not a cleaned or corrected version of a person’s schooling. It is a linear prediction using only experience, IQ, and siblings. For IV to be informative, IQ and siblings must explain enough education variation after experience is held fixed. Flip to step two to see how that predicted component enters the wage equation.
Regress educ on exper, IQ, and sibs:
\begin{align*} educ = \alpha_0 + \alpha_1 exper + \alpha_2 IQ + \alpha_3 sibs + r \end{align*}Use the coefficient estimates on \alpha_0, \alpha_1, \alpha_2, and \alpha_3 to predict educ as a function of exper, IQ, and sibs.
\begin{align*} \widehat{educ} = \widehat{\alpha_0} + \widehat{\alpha_1} exper + \widehat{\alpha_2} IQ + \widehat{\alpha_3} sibs \end{align*}Transcript
The equation now replaces observed education with education hat from the first stage. Log wage remains the dependent variable because that is the structural model we specified. Beta zero is the intercept, beta one multiplies predicted education, beta two multiplies experience, and epsilon is the composite second-stage disturbance. We keep experience in this equation because it is an included exogenous control in the original model.
The code implements that conceptual regression. Fixest double-colon fee-ols estimates log of wage on education underscore hat plus experience, using the columns in wage two, and stores the result as second underscore reg. The final line prints the fitted model. In this sample, the coefficient on predicted education is about 0.147. In a log-wage equation, that corresponds to an approximate 14.7 percent wage difference per additional predicted year of education, or about 15.9 percent using the exact exponential conversion. The experience coefficient is about 0.0357.
Focus on the warning immediately below the output. The coefficient on education underscore hat reproduces the two-stage-least-squares coefficient for the instrument set used in the first stage, but the displayed OLS standard error of about 0.0136 is not the correct two-stage-least-squares standard error. The software has been asked to fit an ordinary regression, so it treats education underscore hat as though it were directly observed and uses the wrong residual variance for IV inference. The command runs without warning, which makes this an easy mistake to miss.
A fee-ols IV formula using this same outcome, controls, and instrument set estimates the same projection-based coefficient and calculates an appropriate two-stage-least-squares variance. In the checked one-call version with IQ and siblings, the education coefficient remains about 0.147, while its proper I I D standard error is about 0.01425 rather than the manual OLS value of about 0.01361. The later syntax demonstration uses a different candidate instrument set, siblings and father’s education, so its numerical coefficient is not intended to match this one. The manual calculation here is for understanding the coefficient, not for reporting uncertainty.
Use \widehat{educ} in place of educ to estimate the model of interest:
\begin{align*} \log(wage) = \beta_0 + \beta_1 \widehat{educ} + \beta_2 exper + \varepsilon \end{align*}The coefficient on educ_hat illustrates the second-stage coefficient. Do not use the standard error from this manually fitted regression; the IV implementation below computes the correct 2SLS variance estimate.
Weak instruments
Transcript
The definition in the first callout is conditional. Excluded instruments are weak when they contribute too little variation in the endogenous regressor after the included exogenous variables, and any fixed effects, have been removed. An instrument can be correlated with x one in the raw data yet become weak in the actual first-stage specification.
Weak is not the same as exactly irrelevant. If the population first-stage coefficient is nonzero but very small, the model may be identified in an asymptotic sense while providing little information in the sample at hand. The fitted movement in x one is then easily overwhelmed by sampling noise. Because 2SLS effectively relates a reduced-form outcome effect to a first-stage regressor effect, a noisy denominator can produce very large and irregular estimates.
The consequences are not limited to a wider standard error. Finite-sample bias can be substantial, point estimates can change dramatically across samples or small specification changes, and the usual normal or t approximations behind Wald tests and confidence intervals can have poor size and coverage. Adding many weak instruments can create further finite-sample problems.
The lower callout gives the correct attitude toward diagnostics. First-stage evidence can reveal a weak-identification concern, but no universal cutoff or single statistic settles every design. Appropriate diagnostics depend on the number of endogenous regressors and instruments, whether errors are heteroskedastic or clustered, and which inferential procedure is being used. The next tabs begin with the familiar joint first-stage test, then show its output in R.
Transcript
The displayed first stage puts education on the left. On the right, alpha zero is the intercept, alpha one multiplies experience, alpha two multiplies siblings, alpha three multiplies father’s education, and v is the first-stage error. Experience is the included exogenous control. Siblings and father’s education are the excluded instruments.
The proposed joint null sets alpha two and alpha three equal to zero. Under that null, once experience is held fixed, neither excluded instrument contributes to the prediction of education. The first-stage F test compares the unrestricted model shown on screen with the restricted model that omits both excluded instruments. Because two restrictions are tested jointly, the numerator degrees of freedom are two; the denominator degrees of freedom depend on the estimation sample and number of estimated first-stage parameters.
Rejecting the null is evidence that the instruments add some predictive content. Failure to reject is strong evidence that they are not useful for conventional IV estimation. But statistical significance is not the same as sufficient strength. With a large enough sample, a substantively tiny first stage can be statistically distinguishable from zero while still producing weak identification for conventional inference.
You may know the rule of thumb that the first-stage F statistic should exceed ten. Treat that as a rough historical diagnostic for relatively simple models with one endogenous regressor and homoskedastic errors, not as a universal pass-fail rule. Robust or clustered settings, multiple endogenous variables, and multiple instruments require diagnostics suited to those conditions. After inspecting the familiar output on the next tab, a serious application should report the appropriate weak-identification measures and, where needed, weak-instrument-robust inference.
Run the first-stage regression:
\begin{align*} educ = \alpha_0 + \alpha_1 exper + \alpha_2 sibs + \alpha_3 feduc + v \end{align*}Then test H_0:\alpha_2=\alpha_3=0 with a first-stage F test.
Rejecting this null establishes that the instruments add some predictive power, but statistical significance alone does not guarantee that the first stage is strong enough for conventional IV inference.
Transcript
The left column shows two ways to inspect the first stage from fixest. Printing I V underscore res displays the structural two-stage-least-squares results and, at the bottom, the first-stage F test for education. In the output we observed, the statistic is about 65.55 with two numerator and 737 denominator degrees of freedom, and the p-value is smaller than conventional reporting precision. Thus we reject the joint null that the coefficients on siblings and father’s education are both zero after controlling for experience.
Open the “Alternatively” panel to inspect the first-stage regression itself. I V underscore res, dollar, I V underscore first underscore stage accesses the stored first-stage component. Because education is the endogenous variable, the component contains a model with education as its dependent variable. The output shows a siblings coefficient of about negative 0.131, a father’s-education coefficient of about positive 0.205, and an experience coefficient of about negative 0.192. The joint F statistic at the bottom is the same 65.55. These are predictive associations in the first stage, not causal effects on education.
Now read every warning in the right callout. The F-greater-than-ten rule is only rough and is not generally calibrated for arbitrary robust or clustered designs. A statistically significant but small F can still indicate weak identification. No first-stage diagnostic provides evidence about exclusion or exogeneity. Failure to reject joint irrelevance is strong negative evidence for conventional IV. Finally, appropriate first-stage and weak-identification diagnostics should be reported, rather than hidden behind a statement that the instruments are “significant.”
For this simple I I D example, the displayed F statistic does not suggest the obvious weak-first-stage failure we will simulate next. It still does not prove the family-background instruments are valid or guarantee every conventional approximation. Strength and validity remain separate questions.
When we estimated the IV model with fixest::feols(), the output included a first-stage F statistic for the excluded instruments.
Here, the F test rejects the null that sibs and feduc have no first-stage explanatory power for educ after controlling for exper.
Alternatively
You can access the iv_first_stage component of the regression results.
Transcript
This simulation is designed to change instrument strength while holding validity and the true causal effect fixed. Set-dot-seed with 73289 makes the random draw reproducible. Capital N is 500, so each vector contains 500 observations. R-uniform, open parenthesis N close parenthesis, draws independent uniform zero-to-one noise each time it is called.
The variable u underscore common is the source shared by the endogenous regressor and the structural error. Z underscore common is a separate random source shared by the endogenous regressor and the instruments. Because those two sources are drawn independently, the instrument source is independent of the outcome error source by construction. X underscore end adds u underscore common, z underscore common, and fresh noise. It is endogenous because its u underscore common component also appears in u. The structural error u adds u underscore common and another independent noise draw.
The strong instrument is z underscore common plus noise, so a substantial part of its variation is shared with x underscore end. The weak instrument is only 0.01 times z underscore common plus 0.99995 times unrelated noise. It is technically connected to x through z underscore common, but that signal is tiny relative to its noise. Both instruments remain valid in the population design because neither contains u underscore common or the other component of u.
The outcome line is y equals x underscore end plus u, so the true structural slope on x is one. The code adds no separate constant, but u is the sum of two uniform zero-to-one variables and therefore has mean one. Because the estimated equation includes an intercept, its population intercept is one when the disturbance is centered to have mean zero. The data-dot-frame call binds y, x, and both instruments into columns for estimation.
The correlation matrix reports sample correlations. In this reproducible draw, y and x correlate about 0.865. The strong instrument correlates about 0.419 with x, while the weak instrument’s sample correlation with x is about negative 0.074 despite its tiny positive population connection. Sampling noise can overwhelm such a weak signal and even reverse its sample sign. That is exactly the instability we want to study. The next tab estimates the same IV equation with each instrument.
Data generation
Correlation
Transcript
The two code blocks estimate exactly the same structural equation, y on the endogenous variable x underscore end plus an intercept. The only change is the excluded instrument after the second tilde. Read the first call as fee-ols of y on one, bar, x underscore end on z underscore strong, using data. The second uses the same IV formula but replaces the final variable with z underscore weak. Each fitted object is passed to tidy, which returns one row per coefficient with the estimate, standard error, test statistic, and p-value.
For the strong instrument, the fitted coefficient on instrumented x is about 1.09 with a conventional standard error of about 0.086. That is reasonably close to the true value of one in this particular sample. The intercept is about 0.88, also reasonably close to its population value of one. That population intercept absorbs the positive mean of u when the regression disturbance is written with mean zero.
For the weak instrument, the x coefficient is about 2.22 with a standard error of about 0.714. It is much farther from the true value even though the usual p-value rejects a zero coefficient. This is a useful warning: statistical significance against zero does not imply that the point estimate is close to the true value, and conventional weak-instrument inference can be misleading.
The answer box describes this draw, not a deterministic rule that every weak-instrument estimate must be large or upward biased. A weak estimate can be too high, too low, or have the opposite sign because the small first-stage signal makes a ratio-like estimator unstable. One realization cannot show the sampling distribution. First compare the two first-stage diagnostics on the next tab, then the Monte Carlo tabs will repeat the whole experiment one thousand times.
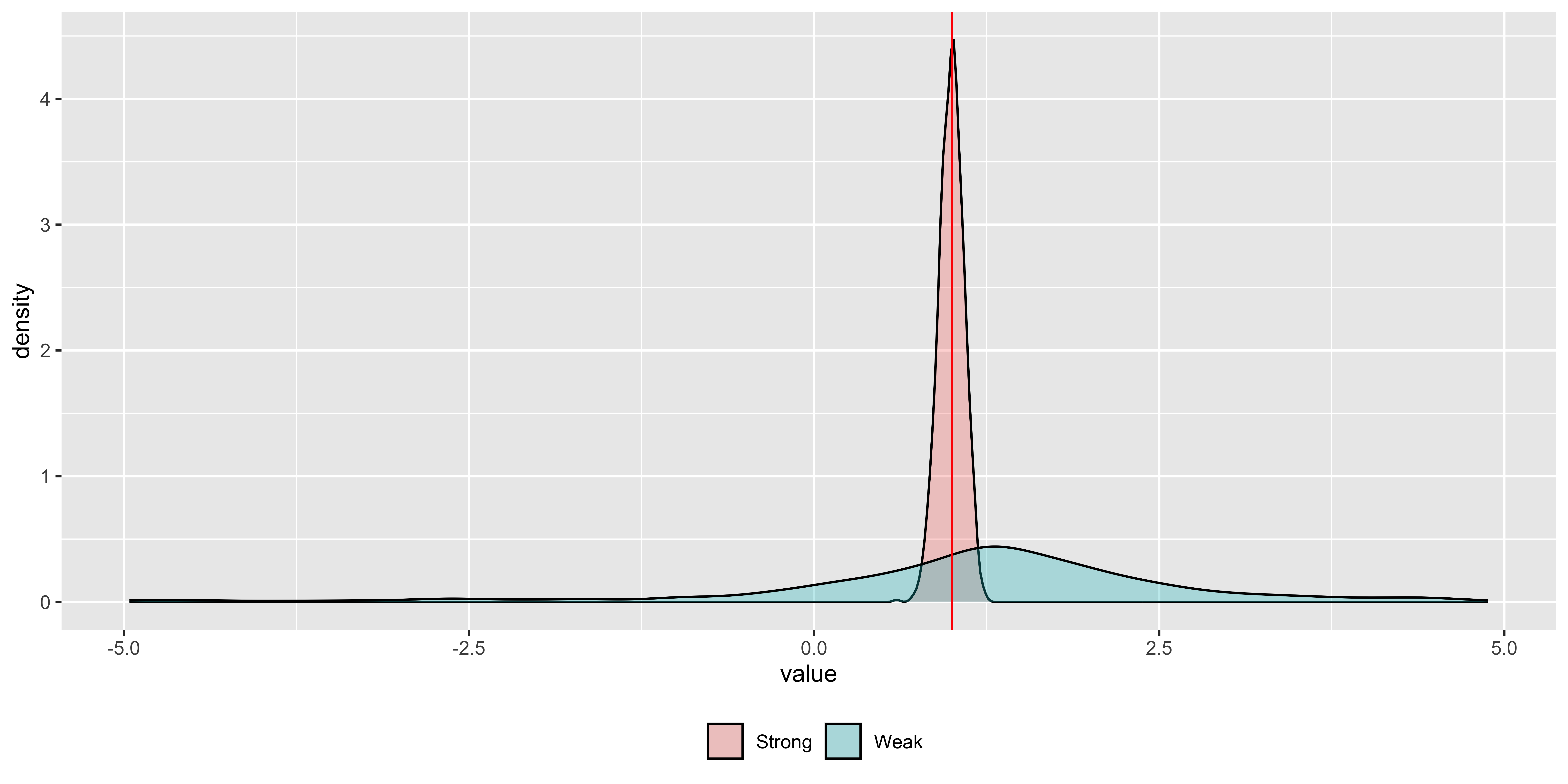
Estimation with the strong instrumental variable
Estimation with the weak instrumental variable
Question
Any notable differences?
Answer
In this draw, the coefficient estimate onx_end is far from the true value in the weak-instrument case. Weak instruments generally produce unstable estimates and unreliable conventional inference.
Transcript
These two columns print the stored first-stage regressions. On the left, I V underscore strong, dollar, I V underscore first underscore stage shows x as the dependent variable and the strong instrument as its excluded predictor. The estimated first-stage coefficient on z underscore strong is about 0.508 with a standard error of about 0.049. The corresponding F statistic is about 106.05 on one and 498 degrees of freedom, with a very small p-value. The adjusted R squared is about 0.174. All of that reflects a visible first-stage signal in the 500 observations.
On the right, the weak first stage looks completely different. The estimated coefficient on z underscore weak is about negative 0.124 with a standard error of about 0.075. Its F statistic is only about 2.76, and its p-value is about 0.097. At the five-percent level, we fail to reject that the excluded instrument has zero first-stage explanatory power. The adjusted R squared is about 0.0035, so the linear fit improves almost nothing after accounting for the intercept.
The negative estimated weak coefficient does not contradict the code’s positive 0.01 loading on z underscore common. That population signal is so small that this sample’s unrelated noise dominates it. This is precisely what weak identification looks like in a finite sample.
These diagnostics concern relevance and strength only. We know both instruments are exogenous here because we wrote the data-generating process and drew their source independently from u underscore common and the remaining outcome noise. In observational work, a first-stage table cannot reveal that fact. The callout summarizes the weak result for this draw. Move to the Monte Carlo run to see why repeated sampling, rather than one unlucky estimate, is the right way to understand the consequence.
diagnostics (strong instrument)
diagnostics (weak instrument)
Transcript
This code repeats the experiment so we can see the sampling distributions. Set-dot-seed with 238354 makes the full sequence reproducible. Capital B is 1,000, the number of simulated experiments, and capital N remains 500 observations per experiment. Matrix, open parenthesis zero comma B comma two close parenthesis, creates a one-thousand-row, two-column storage object. Each row will hold one strong-instrument estimate and one weak-instrument estimate.
The for loop sets i successively from one through B. Inside each iteration, the code redraws u underscore common and z underscore common, constructs endogenous x, constructs the strong and weak instruments with the same loadings as before, builds the structural error, and sets y equal to x plus u. The call to data-dot-table assembles those four variables efficiently for estimation. Because y always has coefficient one on x, the true beta remains one in all one thousand replications. Because the instrument source remains separate from the error source, validity also remains fixed.
The first fee-ols call estimates y on instrumented x using z underscore strong. I V underscore strong, dollar, coefficients returns the coefficient vector, and bracket two selects the second element, the fitted-x coefficient rather than the intercept. The code stores it in row i, column one. The second call repeats the same operation with z underscore weak and stores that fitted-x coefficient in column two. When the loop finishes, every row contains estimates based on the same structural design but a different random sample.
The paired construction isolates the role of strength. We are not changing the causal parameter, the sample size, or instrument validity between the two columns. The next tab reshapes this matrix and plots the distribution of the one thousand estimates for each instrument.
set.seed(238354)
B <- 1000 # the number of experiments
N <- 500 # number of observations
beta_hat_store <- matrix(0, B, 2) # storage of beta hat
for (i in 1:B) {
#--- data generation ---#
u_common <- runif(N)
z_common <- runif(N)
x_end <- u_common + z_common + runif(N)
z_strong <- z_common + runif(N)
z_weak <- 0.01 * z_common + 0.99995 * runif(N)
u <- u_common + runif(N)
y <- x_end + u
data <- data.table(y, x_end, z_strong, z_weak)
#--- IV estimation with a strong instrument ---#
iv_strong <- fixest::feols(y ~ 1 | x_end ~ z_strong, data = data)
beta_hat_store[i, 1] <- iv_strong$coefficients[2]
#--- IV estimation with a weak instrument ---#
iv_weak <- fixest::feols(y ~ 1 | x_end ~ z_weak, data = data)
beta_hat_store[i, 2] <- iv_weak$coefficients[2]
}Transcript
The plotting code first converts the estimate matrix to a data table and then melts its two columns into long form. The generated labels V one and V two are replaced by “Strong” and “Weak” using data table’s bracket and colon-equals update syntax. Each resulting row contains an instrument-strength label and one estimated coefficient.
The G G plot call filters to estimates with absolute value below five so the central part of the figure remains readable. Geom-density puts the coefficient estimate on the horizontal axis and estimated probability density on the vertical axis. Fill color distinguishes the Strong and Weak distributions, and alpha 0.3 makes the overlapping filled curves transparent. Geom-v-line draws the red vertical reference line at one, the true structural coefficient. The discrete fill scale removes the legend title, the lecture theme sets the common slide appearance, and the final theme call moves the legend below the plot.
What should you see? The strong-instrument density is narrow and centered close to the red line. Across the checked replications, its estimates range from about 0.60 to 1.25, with a standard deviation of about 0.089. The weak-instrument estimates are much more dispersed and irregular. Their median is about 1.33, their standard deviation is about 16.1, and extreme values range below negative 319 and above positive 158.
The caption warns that the displayed graph omits estimates with absolute value greater than five. In this run, 98 of the 1,000 weak-instrument estimates are outside that plotting window, while none of the strong-instrument estimates are. Those omitted values are not harmless outliers to discard from the statistical conclusion. They are direct evidence of the heavy-tailed, unstable sampling behavior created by a nearly zero first stage.
The instruments are valid by construction and the weak one is technically relevant in the population, yet conventional estimation behaves poorly because it predicts too little of x. That is why weak identification calls for appropriate diagnostics and, when necessary, weak-instrument-robust inference rather than confidence based on a significant second-stage coefficient.
Code
melted <- melt(data.table(beta_hat_store))
melted[variable == "V1", variable := "Strong"]
melted[variable == "V2", variable := "Weak"]
ggplot(data = melted[abs(value) < 5, ]) +
geom_density(aes(x = value, fill = variable), alpha = 0.3) +
geom_vline(xintercept = 1, color = "red") +
scale_fill_discrete(name = "") +
theme_lecture +
theme(
legend.position = "bottom"
)
The plot omits estimates with absolute value greater than 5 so that the central portions of the distributions remain visible; extreme estimates are themselves a symptom of weak identification.