| Location | Year | P | Q |
|---|---|---|---|
| Chicago | 2003 | 75 | 2.0 |
| Peoria | 2003 | 50 | 1.0 |
| Milwaukee | 2003 | 60 | 1.5 |
| Madison | 2003 | 55 | 0.8 |
10: Panel Data Methods
Panel (longitudinal) Data Methods
Definition
Data follow the same individuals, families, firms, cities, states or whatever, across time.
Example
Randomly select people from a population at a given point in time
Then the same people are reinterviewed at several subsequent points in time, which would result in data on wages, hours, education, and so on, for the same group of people in different years.
Panel Data as data.frame
year: yearfcode: factory idemploy: the number of employeessales: sales in USD
Can we do anything to deal with endogeneity problem taking advantage of the panel data structure?
Panel Data Estimation Methods
Demand for massage (cross-sectional)
P: the price of one massageQ: the number of massages received per capita
Across the four cities, how are price and quantity are associated? Positive or negative?
Answer
They are positively correlated. So, does that mean people want more massages as their price increases? Probably not.What could be causing the positive correlation?
Answer
- Income (can be observed)
- Quality of massages (hard to observe)
- How physically taxing jobs are (?)
Demand for massage (cross-sectional)
| Location | Year | P | Q | Ql |
|---|---|---|---|---|
| Chicago | 2003 | 75 | 2.0 | 10 |
| Peoria | 2003 | 50 | 1.0 | 5 |
| Milwaukee | 2003 | 60 | 1.5 | 7 |
| Madison | 2003 | 55 | 0.8 | 6 |
Key
Massage quality was hidden (omitted) affecting both price and massages per capita.
Problem
Massage quality is not observable, and thus cannot be controlled for.
Mathematically
\(Q = \beta_0 + \beta_1 P + v \;\;( = \beta_2 + Ql + u)\)
- \(P\): the price of one massage
- \(Q\): the number of massages received per capita
- \(Ql\): the quality of massages
- \(u\): everything else that affect \(P\)
Endogeneity Problem
\(P\) is correlated with \(Ql\).
| Location | Year | P | Q | Ql |
|---|---|---|---|---|
| Chicago | 2003 | 75 | 2.0 | 10 |
| Chicago | 2004 | 85 | 1.8 | 10 |
| Peoria | 2003 | 50 | 1.0 | 5 |
| Peoria | 2004 | 48 | 1.1 | 5 |
| Milwaukee | 2003 | 60 | 1.5 | 7 |
| Milwaukee | 2004 | 65 | 1.4 | 7 |
| Madison | 2003 | 55 | 0.8 | 6 |
| Madison | 2004 | 60 | 0.7 | 6 |
There are two kinds of variations:
- inte-rcity (across city) variation
- intra-city (within city) variation
The cross-sectional data offers only the inte-rcity (across city) variations.
Now, compare the massage price and massages per capita within each city (over time). What do you see?
Answer
Price and quantity are negatively correlated!Why looking at the intra-city (within city) variation seemed to help us estimate the impact of massage price on demand more credibly?
Answer
The omitted variable, massage quality, did not change over time within city, which means it is controlled for as long as you look only at the intra-city variations (you do not compare across cities).Using only the intra-city variations
Question
So, how do we use only the intra-city variations in a regression framework?
first-differencing
One way to do this is to compute the changes in prices and th changes in quantities in each city \((\Delta P\) and \(\Delta Q)\) and then regress \(\Delta Q\) and \(\Delta P\).
First-differenced Data
| Location | Year | P | Q | Ql | P_dif | Q_dif | Ql_dif |
|---|---|---|---|---|---|---|---|
| Chicago | 2003 | 75 | 2.0 | 10 | NA | NA | NA |
| Chicago | 2004 | 85 | 1.8 | 10 | 10 | -0.2 | 0 |
| Peoria | 2003 | 50 | 1.0 | 5 | NA | NA | NA |
| Peoria | 2004 | 48 | 1.1 | 5 | -2 | 0.1 | 0 |
| Milwaukee | 2003 | 60 | 1.5 | 7 | NA | NA | NA |
| Milwaukee | 2004 | 65 | 1.4 | 7 | 5 | -0.1 | 0 |
| Madison | 2003 | 55 | 0.8 | 6 | NA | NA | NA |
| Madison | 2004 | 60 | 0.7 | 6 | 5 | -0.1 | 0 |
Key
Variations in quality is eliminated after first differentiation!! (quality is controlled for)
A new way of writing a model
\(Q_{i,t} = \beta_0 + \beta_1 P_{i,t} + v_{i,t} \;\; ( = \beta_2 Ql_{i,t} + u_{i,t})\)
i: indicates cityt: indicates time
First differencing
\(Q_{i,1} = \beta_0 + \beta_1 P_{i,1} + v_{i,1} \;\; ( = \beta_2 Ql_{i,1} + u_{i,1})\)
\(Q_{i,2} = \beta_0 + \beta_1 P_{i,2} + v_{i,2} \;\; ( = \beta_2 Ql_{i,2} + u_{i,2})\)
\(\Rightarrow\)
\(\Delta Q = \beta_1 \Delta P + \Delta v ( = \beta_2 \Delta Ql + \Delta u)\)
Endogeneity Problem?
Since \(Ql_{i,1} = Ql_{i,2}\), \(\Delta Ql = 0 \Rightarrow \Delta Q = \beta_0 + \beta_1 \Delta P + \Delta u\)
No endogeneity problem after first differentiation!
Data
OLS on the original data:
OLS on the first-differenced data:
As long as the omitted variable that affects both the dependent and independent variables are constant over time (time-invariant), then using only the variations over time (ignoring variations across cross-sectional units) can eliminate the omitted variable bias
First-differencing the data and then regressing changes on changes does the trick of ignoring variations across cross-sectional units
Of course, first-differencing is possible only because the same cross-sectional units are observed multiple times over time.
Multi-year (general) panel datasets
within-transformation
If we have lots of years of data, we could, in principle, compute all of the first differences (i.e., 2004 versus 2003, 2005 versus 2004, etc.) and then run a single regression. But there is an easier way.
Instead of thinking of each year’s observation in terms of how much it differs from the prior year for the same city, let’s think about how much each observation differs from the average for that city.
Example
How much each observation differs from the average for that city?
| Location | Year | P | P_mean | P_dev | Q | Q_mean | Q_dev | Ql | Ql_mean | Ql_dev |
|---|---|---|---|---|---|---|---|---|---|---|
| Chicago | 2003 | 75 | 80.0 | -5.0 | 2.0 | 1.90 | 0.10 | 10 | 10 | 0 |
| Chicago | 2004 | 85 | 80.0 | 5.0 | 1.8 | 1.90 | -0.10 | 10 | 10 | 0 |
| Peoria | 2003 | 50 | 49.0 | 1.0 | 1.0 | 1.05 | -0.05 | 5 | 5 | 0 |
| Peoria | 2004 | 48 | 49.0 | -1.0 | 1.1 | 1.05 | 0.05 | 5 | 5 | 0 |
| Milwaukee | 2003 | 60 | 62.5 | -2.5 | 1.5 | 1.45 | 0.05 | 7 | 7 | 0 |
| Milwaukee | 2004 | 65 | 62.5 | 2.5 | 1.4 | 1.45 | -0.05 | 7 | 7 | 0 |
| Madison | 2003 | 55 | 57.5 | -2.5 | 0.8 | 0.75 | 0.05 | 6 | 6 | 0 |
| Madison | 2004 | 60 | 57.5 | 2.5 | 0.7 | 0.75 | -0.05 | 6 | 6 | 0 |
Note
We call this data transformation within-transformation or demeaning .
Model
- Dependent variable:
Q_dev - Independent variable:
P_dev
Key
In calculating P_dev (deviation from the mean by city), Ql_dev is eliminated.
\(Q_{i,1} = \beta_0 + \beta_1 P_{i,1} + v_{i,1} \;\; ( = \beta_2 Ql_{i,1} + u_{i,1})\)
\(Q_{i,2} = \beta_0 + \beta_1 P_{i,2} + v_{i,2} \;\; ( = \beta_2 Ql_{i,2} + u_{i,2})\)
\(\vdots\)
\(Q_{i,T} = \beta_0 + \beta_1 P_{i,T} + v_{i,T} \;\; ( = \beta_2 Ql_{i,T} + u_{i,T})\)
\(\Rightarrow\)
\(Q_{i,t} - \bar{Q_{i}} = \beta_1 [P_{i,t} - \bar{P_{i}}] + [v_{i,t} - \bar{v_{i}}] ( = \beta_2 [Ql_{i,t} - \bar{Ql_{i}}] + [u_{i,t} - \bar{u_{i}}])\)
\(Ql_{i,1} = Ql_{i,2} = \dots = Ql_{i,T} = \bar{Ql_i}\)
\(\Rightarrow\)
\(Q_{i,t} - \bar{Q_{i}} = \beta_1 [P_{i,t} - \bar{P_{i}}] + [u_{i,t} - \bar{u_{i}}]\)
No endogeneity problem after the within-transformation because \(Ql\) is gone.
Fixed Effects (FE) Estimation (in general)
Consider the following general model
\(y_{i,t}=\beta_1 x_{i,t} + \alpha_i + u_{i,t}\)
- \(\alpha_i\): the impact of time-invariant unobserved factor that is specific to \(i\) (also termed individual fixed effect)
- \(\alpha_i\) is thought to be correlated with \(x_{i,t}\)
For each \(i\), average this equation over time, we get
\(\frac{\sum_{t=1}^T y_{i,t}}{T} = \frac{\sum_{t=1}^T x_{i,t}}{T} + \alpha_i + \frac{\sum_{t=1}^T u_{i,t}}{T}\)
We use \(\bar{z}_i\) to indicate the average of \(\bar{z}_{i,t}\) over time for individual \(i\). Using this notation,
\(\bar{y}_i = \bar{x}_i + \alpha_i + \bar{u}_i\)
Note that \(\frac{\sum_{t=1}^T \alpha_{i}}{T} = \alpha_i\)
Subtracting the equation of the average from the original model,
\((y_{i,t}-\bar{y}_i=\beta_1 (x_{i,t} -\bar{x}_i) + (u_{i,t} -\bar{u}_i) + a_i - a_i\)
Important
\(\alpha_i\) is gone!
We then regress \((y_{i,t}-\bar{y}_i)\) on \((x_{i,t}-\bar{x}_i)\) to estimate \(\beta_1\).
Here is the model after within-transformation:
\[\begin{align*} y_{i,t}-\bar{y}_i=\beta_1 (x_{i,t} -\bar{x}_i) + (u_{i,t} -\bar{u}_i) \end{align*}\]So,
\(x_{i,t} -\bar{x}_i\) needs to be uncorrelated with \(u_{i,t} -\bar{u}_i\).
Important
The above condition is satisfied if
\(E[u_{i,s}|x_{i,t}] = 0 \;\; ^\forall s, \;\; t, \;\;\mbox{and} \;\;j\)
e.g., \(E[u_{i,1}|x_{i,4}]=0\)
Fixed effects estimation
Regress within-transformed Q on within-transformed P:
An alternative way to view the Fixed Effects estimation methods
Important
The two approaches below will result in the same coefficient estimates (mathematically identical).
- Running OLS on the within-tranformed (demeaned) data
- Running OLS on the untransformed data but including the dummy variables for the individuals (city in our example)
You can use the original data (no within-transformation) and include dummy variables for all the cities except one.
Note that the coefficient estimate on P is exactly the same as the one we saw earlier when we regressed Q_dev on P_dev.
By including individual dummies (individual fixed effects), you are effectively eliminating the between (inter-city) variations and using only the clean within (within-city) variations for estimation.
Very Important
More generally, including dummy variables of a categorical variable (like city in the example above), eliminates the variations between the elements of the category (e.g., different cities), and use only the variations within each of the element of the category.
Fixed Effects Estimation in Practice Using R
Advice
- Do not within-transform the data yourself and run a regression
- Do not create dummy variables yourself and run a regression with the dummies
In practice
We will use the fixest package.
Syntax
FE: the name of the variable that identifies the cross-sectional units that are observed over time (Locationin our example)dep_var: (non-transformed) dependet variableindep_vars: list of (non-transformed) independent variables
Data
Example
How is it different from the FE model?
Can be more efficient (lower variance) than FE under certain cases
If \(\alpha_i\) and independent variables are correlated, then RE estimators are biased
Unless \(\alpha_i\) and independent variables are not correlated (which does not hold most of the time unless you got data from controlled experiments), \(RE\) is not an attractive option
You almost never see this estimation method used in papers that use non-experimental data
Note
We do not cover this estimation method as you almost certainly would not use this estimation method.
Fixed effects (dummy variables) to harness clean variations
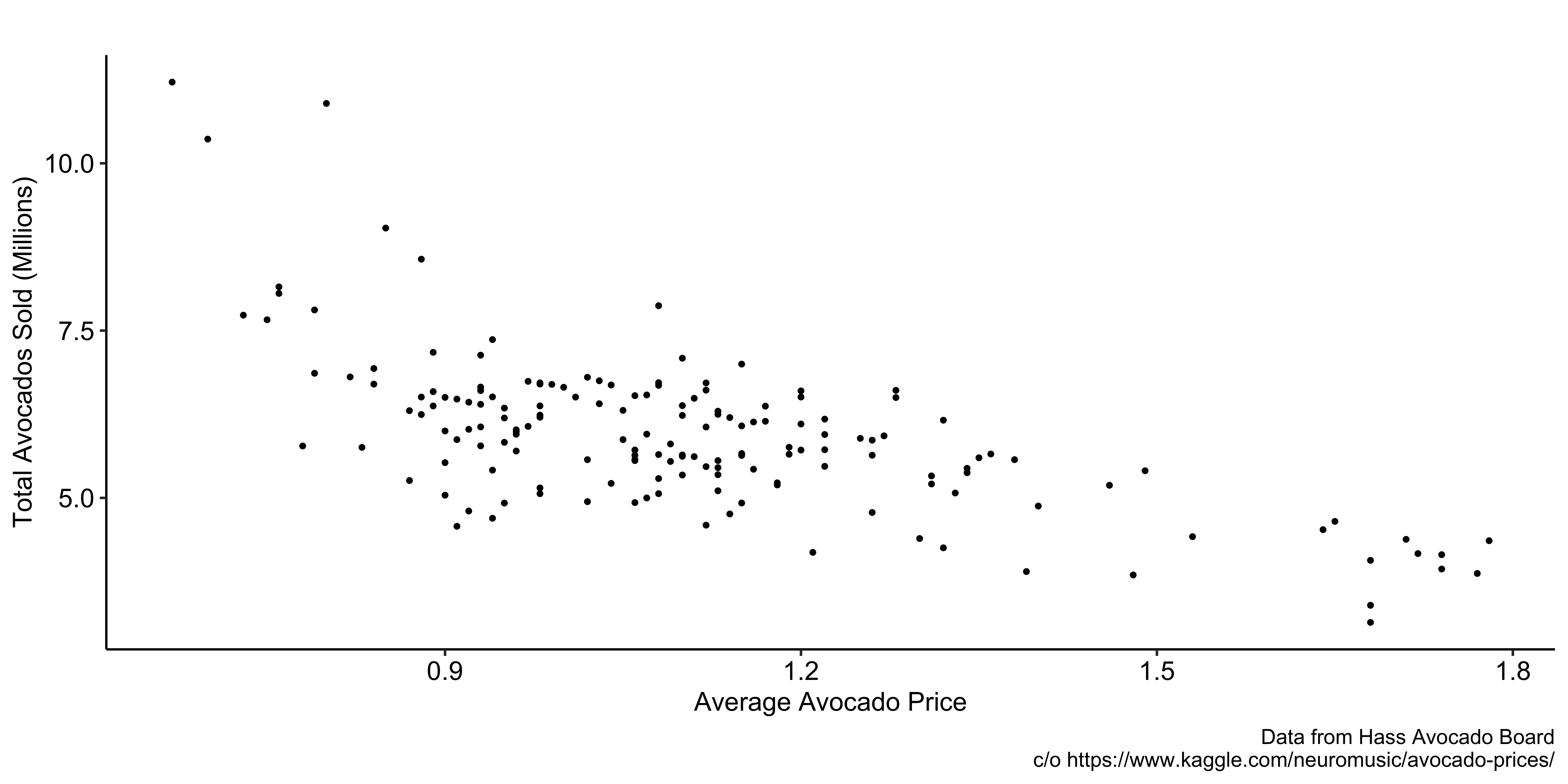
Objective
You are interested in understanding the impact of avocado price on its consumption.
Observations
- They are negatively associated with each other
- Avocado sales tend to be lower in weeks where the price of avocados is high.
- Prices tend to be higher in weeks where fewer avocados are sold
Question
If you just regress avocado sales on its price, is the estimation of the coefficient on the pirce unbiased?
Answer
No.
- Reverse causality
- price affects demand
- demand affects price
Problem
Reverse Causality: Price affects demand and demand affects price.
contextual knowledge
Now, suppose you learned the following fact after studying the supply and purchasing mechanism on the avocado market:
At the beginning of each month, avocado suppliers make a plan for what avocado prices will be each week in that month, and never change their plans until the next month.
This means that within the same month changes in avocado price every week is not a function of how much avocado has been bought in the previous weeks, effectively breaking the causal effect of demand on price.
So, our estimation strategy would be to just look at the variations in demand and price within individual months, but ignore variations in price between months.
The figure below presents avocado sales and price of avocado in March, 2015. This is an example of clean variations in price (intra-month observations).
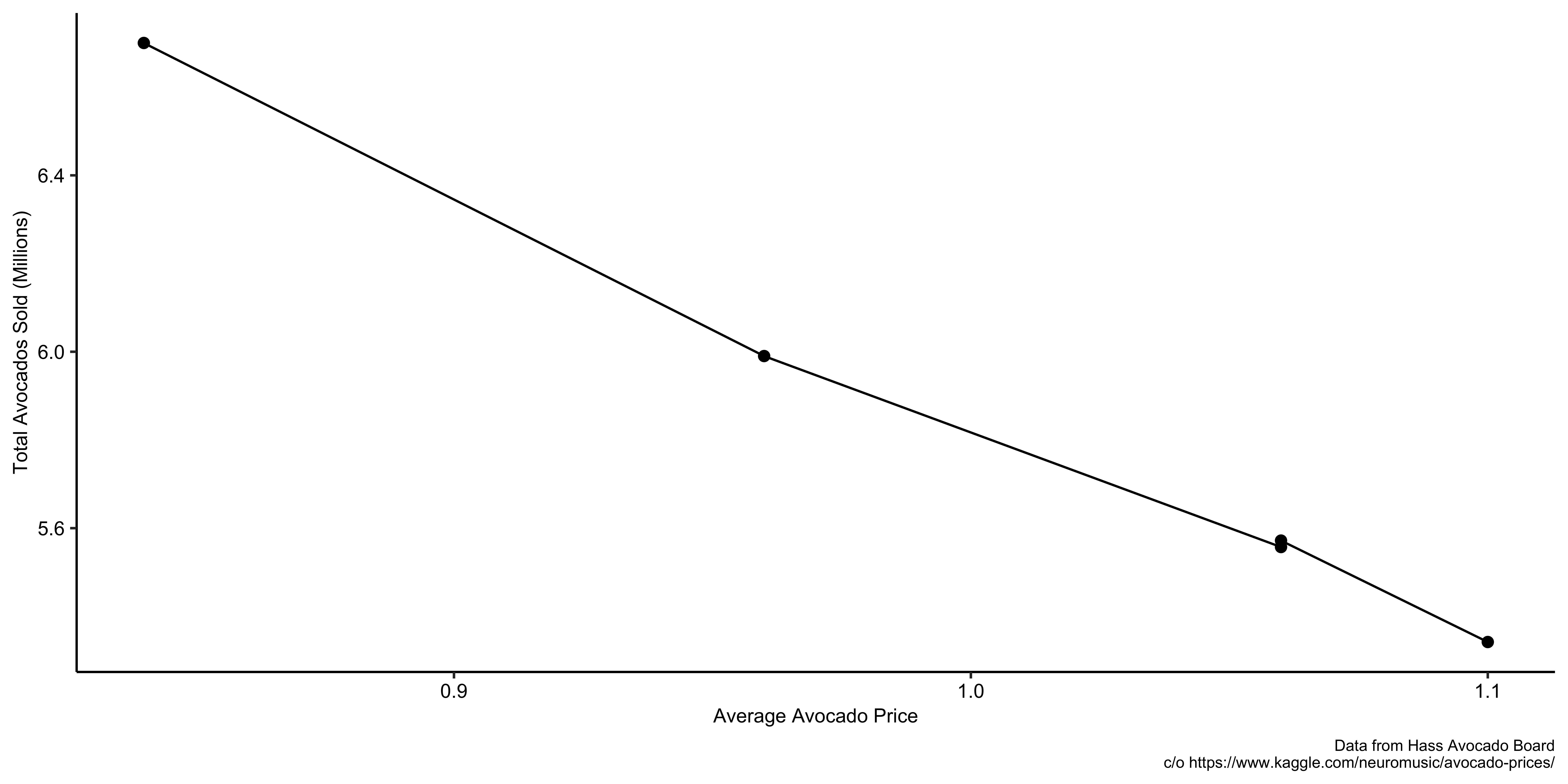
We have three months of avocado purchase and price observed weekly.
Question
What should we do?
Answer
Include month dummy variables.We have two years of avocado purchase and price observed weekly.
Question
What should we do?
Answer
Include month-year dummy variables.
Including month dummy variables will not do it. Because the observations in the same month in two different years are considered to belong to the same group. That is, variations between two different years of the same month will be used for estimation. (e.g., January in 2014 and January in 2015)
Message 1
By understanding the data generating process (knowing how any economic market works), we recognize the problem of simply looking at the relationship between the avocado price and demand to conclude the causal impact of price on demand (reverse causality).
Message 2
We study the context very well and how the avocado market works in California (of course it is not really how CA avocado market works in reality) and make use of the information to identify the “clean” variations in avocado price to identify its impact on demand.
Year Fixed Effects
Just a collection of year dummies, which takes 1 if in a specific year, 0 otherwise.
They capture anything that happened to all the individuals for a specific year relative to the base year
Example
Education and wage data from \(2012\) to \(2014\),
\(log(income) = \beta_0 + \beta_1 educ + \beta_2 exper + \sigma_1 FE_{2012} + \sigma_2 FE_{2013}\)
\(\sigma_1\): captures the difference in \(log(income)\) between \(2012\) and \(2014\) (base year)
\(\sigma_2\): captures the difference in \(log(income)\) between \(2013\) and \(2014\) (base year)
Interpretation
\(\sigma_1=0.05\) would mean that \(log(income)\) is greater in \(2012\) than \(2014\) by \(5\%\) on average for whatever reasons with everything else fixed.
Recommendation
It is almost always a good practice to include year FEs if you are using a panel dataset with annual observations.
Why?
Remember year FEs capture anything that happened to all the individuals for a specific year relative to the base year
In other words, all the unobserved factors that are common to all the individuals in a specific year is controlled for (taken out of the error term)
Example
Economic trend in:
\(log(income) = \beta_0 + \beta_1 educ + \sigma_1 FE_{2012} + \sigma_2 FE_{2013}\)
Education is non-decreasing through time
Economy might have either been going down or up during the observed period
Without year FE, \(\beta_1\) may capture the impact of overall economic trend.
In order to include year FEs to individual FEs, you can simply add the variable that indicates year like below:
Caveats
Year FEs would be perfectly collinear with variables that change only across time, but not across individuals.
If your variable of interest is such a variable, you cannot include year FEs, which would then make your estimation subject to omitted variable bias due to other unobserved yearly-changing factors.
Standard Error Estimation for Panel Data Methods
Heteroskedasticity
Just like we saw for OLS using cross-sectional data, heteroskedasticity leads to biased estimation of the standard error of the coefficient estimators if not taken into account
Serial Correlation
Correlation of errors over time, which we call serial correlation
just like heteroskedasticity, serial correlation could lead to biased estimation of the standard error of the coefficient estimators if not taken into account
do not affect the unbiasedness and consistency property of your estimators
Important
Taking into account the potential of serial correlation when estimating the standard error of the coefficient estimators can dramatically change your conclusions about the statistical significance of some independent variables!!
When serial correlation is ignored, you tend to underestimate the standard error (why?), inflating \(t\)-statistic, which in turn leads to over-rejection that you should.
Bertrand, Duflo, and Mullainathan (2004)
Examined how problematic serial correlation is in terms of inference via Monte Carlo simulation
generate a fake treatment dummy variable in a way that it has no impact on the outcome (dependent variable) in the dataset of women’s wages from the Current Population Survey (CPS)
run regression of the oucome on the treatment variable
test if the treatment variable has statistically significant effect via \(t\)-test
They rejected the null \(67.5\%\) at the \(5\%\) significance level!!
SE robust to heteroskedasticity and serial correlation
You can take into account both heteroskedasticity and serial correlation by clustering by individual (whatever the unit of individual is: state, county, farmer)
Cluster by individual can take into account the correlation within individuals (over time)
R implementation
The last partition is used for clustering standard error estimation by variable like below.