08: OLS Asymptotics

OLS Asymptotics

Large Sample Properties of OLS

Properties of OLS that hold only when the sample size is infinite
(loosely put) How OLS estimators behave when the number of observations goes infinite (really large)

Small Sample Properties of OLS

Under certain conditions:

OLS estimators are unbiased
OLS estimators are efficient

These hold whatever the sample size is .

Consistency

Definition
MC simulation
MC simualation: Inconsistency

Verbally (and very loosely)

An estimator is consistent if the probability that the estimator produces the true parameter is 1 when sample size is infinite.

Setup
Conceptual steps (Pseudo Code)
R code
Results

OLS estimator of the coefficient on \(x\) in the following model with all \(MLR.1\) through \(MLR.4\) satisfied:

\[y_i = \beta_0 + \beta_1 x_i + u_i\]

with all the conditions necessary for the unbiasedness property of OLS satisfied.

Generate data according to \(y_i = \beta_0 + \beta_1 x_i + u_i\)
Estimate the coefficients and store them
Repeat the above experiment 1000 times
Examine how the coefficient estimates are distributed

What you should see is

As \(N\) gets larger (more observations), the distribution of \(\widehat{\beta}_1\) get more tightly centered around its true value (here, \(1\)). Eventually, it becomes so tight that the probability you get the true value becomes 1.

Consistency of OLS estimators

Under \(MLR.1\) through \(MLR.4\), OLS estimators are consistent

Conceptual steps (Pseudo Code)
R code
Results

Pseudo Code

generate data (\(N\) observations) according to \(y_i = \beta_0 + \beta_1 x_i + u_i\) with \(E[u_i|x_i]\ne 0\)
Estimate the coefficients and store them
repeat the above experiment 1000 times
examine how the coefficient estimates are distributed

Question

Would the bias disappear as N gets larger?

Asymptotic Normality

Normality assumption
Central Limit Theorem (CLT)
Demonstration
OLS estimator

When we talked about hypothesis testing, we made the following assumption:

Normality assumption

The population error \(u\) is independent of the explanatory variables \(x_1,\dots,x_k\) and is normally distributed with zero mean and variance \(\sigma^2\):

\(u\sim Normal(0,\sigma^2)\)

Remember

If the normality assumption is violated, t-statistic and F-statistic we constructed before are no longer distributed as t-distribution and F-distribution, respectively
So, whenever \(MLR.6\) is violated, our t- and F-tests are invalid

Fortunately

You can continue to use t- and F-tests because (slightly transformed) OLS estimators are approximately normally distributed when the sample size is large enough.

Central Limit Theorem

Suppose \(\{x_1,x_2,\dots\}\) is a sequence of idetically independently distributed random variables with \(E[x_i]=\mu\) and \(Var[x_i]=\sigma^2<\infty\). Then, as \(n\) approaches infinity,

\[\sqrt{n}(\frac{1}{n} \sum_{i=1}^n x_i-\mu)\overset{d}{\longrightarrow} N(0,\sigma^2)\]

Verbally

Sample mean less its expected value multiplied by \(\sqrt{n}\) (square root of the sample size) is going to be distributed as Normal distribution as \(n\) goes infinity where its expected value is 0 and variance is the variance of \(x\).

Example
Demonstration

Setup

Conside a random variable (\(x\)) that follows Bernouli distribution with \(p = 0.3\). That is, it takes 0 and 1 with probability of 0.7 and 0.3, respectively.

\(x_i \sim Bern(p = 0.3)\)

\(\mu = E[x_i] = p = 0.3\)
\(\sigma^2 \equiv Var[x_i] = p(1-p) = 0.21\)

This is what 10 random draws and the transformed version of their sum look like:

According to CLT

\(\sqrt{n}(\frac{1}{n} \sum_{i=1}^n x_i-\mu)\overset{d}{\longrightarrow} N(0,\sigma^2)\)

So,

\(\sqrt{n}(\frac{1}{n} \sum_{i=1}^n x_i-0.3)\overset{d}{\longrightarrow} N(0,0.21)\)

In each of the 5000 iterations, this application draws the number of samples you specify (\(N\)) from \(x_i \sim Bern(p=0.3)\) and then calculate \(\sqrt{N}(\frac{1}{N} \sum_{i=1}^N x_i-0.3)\). Then the histogram of the 5000 values is presented.

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| standalone: true

library(shiny)
library(ggplot2)
library(bslib)

# Define UI for CLT demonstration

ui <- page_sidebar(
  title = "CLT demonstration",
  sidebar = sidebar(
    numericInput("n_samples",
        "Number of samples:",
        min = 1, max = 100000, value = 10, step = 100
      ),
    br(),
    actionButton("simulate", "Simulate"),
    open = TRUE
  ),
  plotOutput("cltPlot")
)

# Define server logic to simulate the Central Limit Theorem
server <- function(input, output) {
  observeEvent(input$simulate, {
    output$cltPlot <- renderPlot({
      N <- input$n_samples # number of observations #<<
      B <- 5000 # number of iterations
      p <- 0.3 # mean of the Bernoulli distribution
      storage <- rep(0, B)

      for (i in 1:B) {
        #--- draw from Bern[0.3] (x distributed as Bern[0.3]) ---#
        x_seq <- runif(N) <= p

        #--- sample mean ---#
        x_mean <- mean(x_seq)

        #--- normalize ---#
        lhs <- sqrt(N) * (x_mean - p)

        #--- save lhs to storage ---#
        storage[i] <- lhs
      }

      #--- create a figure to present ---#
      ggplot() +
        geom_histogram(
          data = data.frame(x = storage),
          aes(x = x),
          color = "blue",
          fill = "gray"
        ) +
        xlab("Transformed version of sample mean") +
        ylab("Count") +
        theme_bw()
    })
  })
}

# Run the application
shinyApp(ui = ui, server = server)

Asymptotic normality
test-statistic (small v.s. large sample)

Under assumptions \(MLR.1\) through \(MLR.5\), with any distribution of the error term (the normality assumption of the error term not necessary), OLS estimator is asymptotically normally distributed.

Asymptotic Normality of OLS

\(\sqrt{n}(\widehat{\beta}_j-\beta_j)\overset{a}{\longrightarrow} N(0,\sigma^2/\alpha_j^2)\)

where \(\alpha_j^2=plim(\frac{1}{n}\sum_{i=1}^n r^2_{i,j})\), where \(r^2_{i,j}\) are the residuals from regressing \(x_j\) on the other independent variables.

Consistency

\(\widehat{\sigma}^2\equiv \frac{1}{n-k-1}\sum_{i=1}^n \widehat{u}_i^2\) is a consistent estimator of of \(\sigma^2\) \((Var(u))\)

Small sample (any sample size)

Under \(MLR.1\) through \(MLR.5\) and \(MLR.6\) \((u_i\sim N(0,\sigma^2))\),

\((\widehat{\beta}_j-\beta_j)/se(\widehat{\beta}_j) \sim N(0,1)\)
\((\widehat{\beta}_j-\beta_j)/\widehat{se(\widehat{\beta}_j)} \sim t_{n-k-1}\)

Large sample (when \(n\) goes infinity)

Under \(MLR.1\) through \(MLR.5\) without \(MLR.6\),

\((\widehat{\beta}_j-\beta_j)/se(\widehat{\beta}_j) \overset{a}{\longrightarrow} N(0,1)\)
\((\widehat{\beta}_j-\beta_j)/\widehat{se(\widehat{\beta}_j)} \overset{a}{\longrightarrow} N(0,1)\)

It turns out,

You can proceed exactly the same way as you did before (practically speaking)!!

calculate \((\widehat{\beta}_j-\beta_j)/\widehat{se(\widehat{\beta}_j)}\)
check if the obtained value is greater than (in magnitude) the critical value for the specified significance level under \(t_{n-k-1}\)

But,

Shouldn’t we use \(N(0,1)\) when you find the critical value?

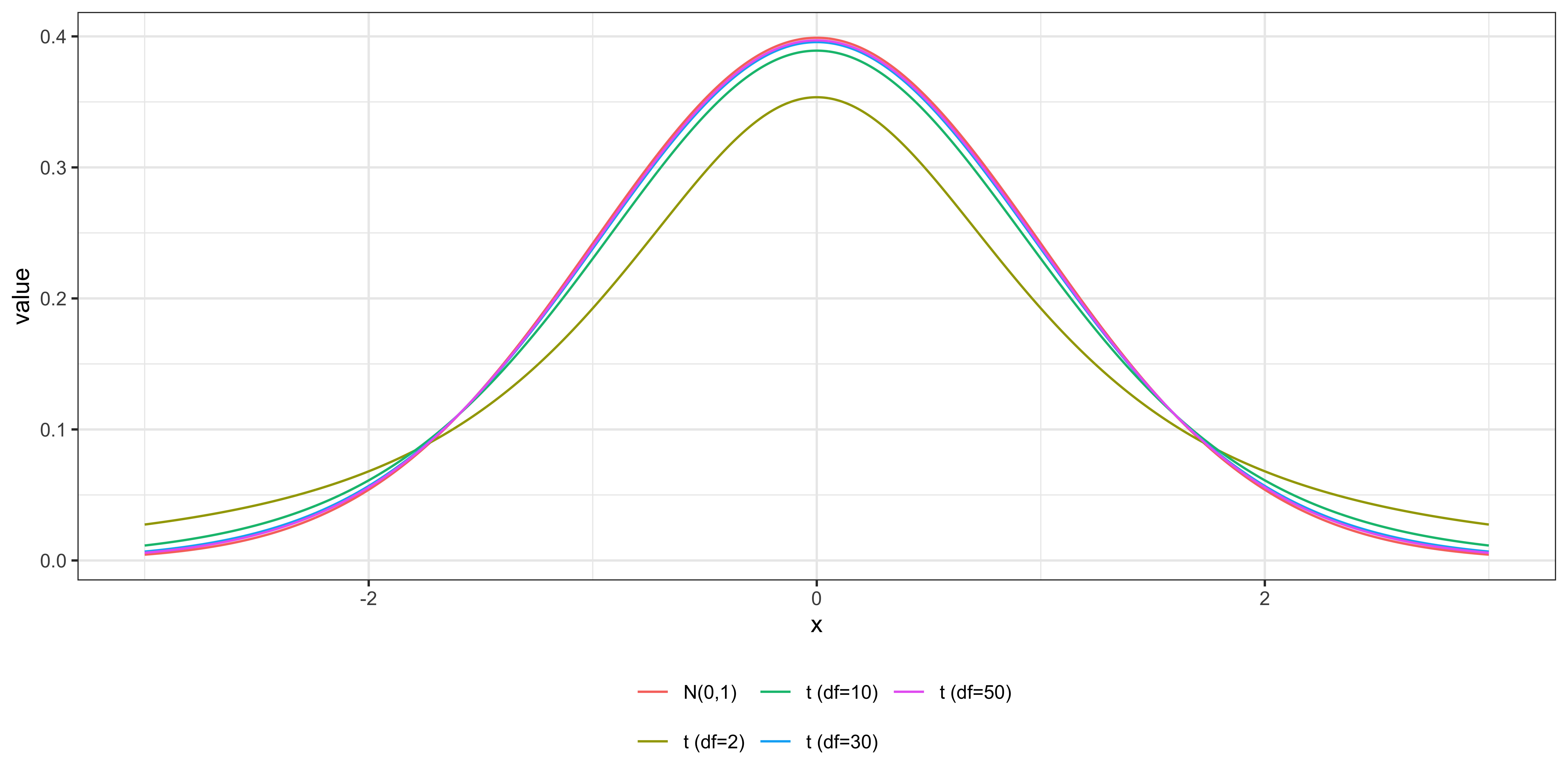
Since \(t_{n-k-1}\) and \(N(0,1)\) are almost identical when \(n\) is large, there is very little error in using \(t_{n-k-1}\) instead of \(N(0,1)\) to find the critical value.

The consistency of the default estimation of \(\widehat{Var(\widehat{\beta})}\) DOES require the homoskedasticity assumption (MLR.5).

In other words, the problem of using the default variance estimator under the hteroskedasticity does not go away even when the sample size is large.

So, we should use heteroskedasticity-robust or cluster-robust standard error estimators even when the sample size is large