07: Econometric Modeling

Functional form

Introduction
Linear or Non-linear?
Why bother?

Transformation of variables is allowed without disturbing our analytical framework as long as the model is linear in parameter .
Transformation of variables change the interpretation of the coefficients estimates

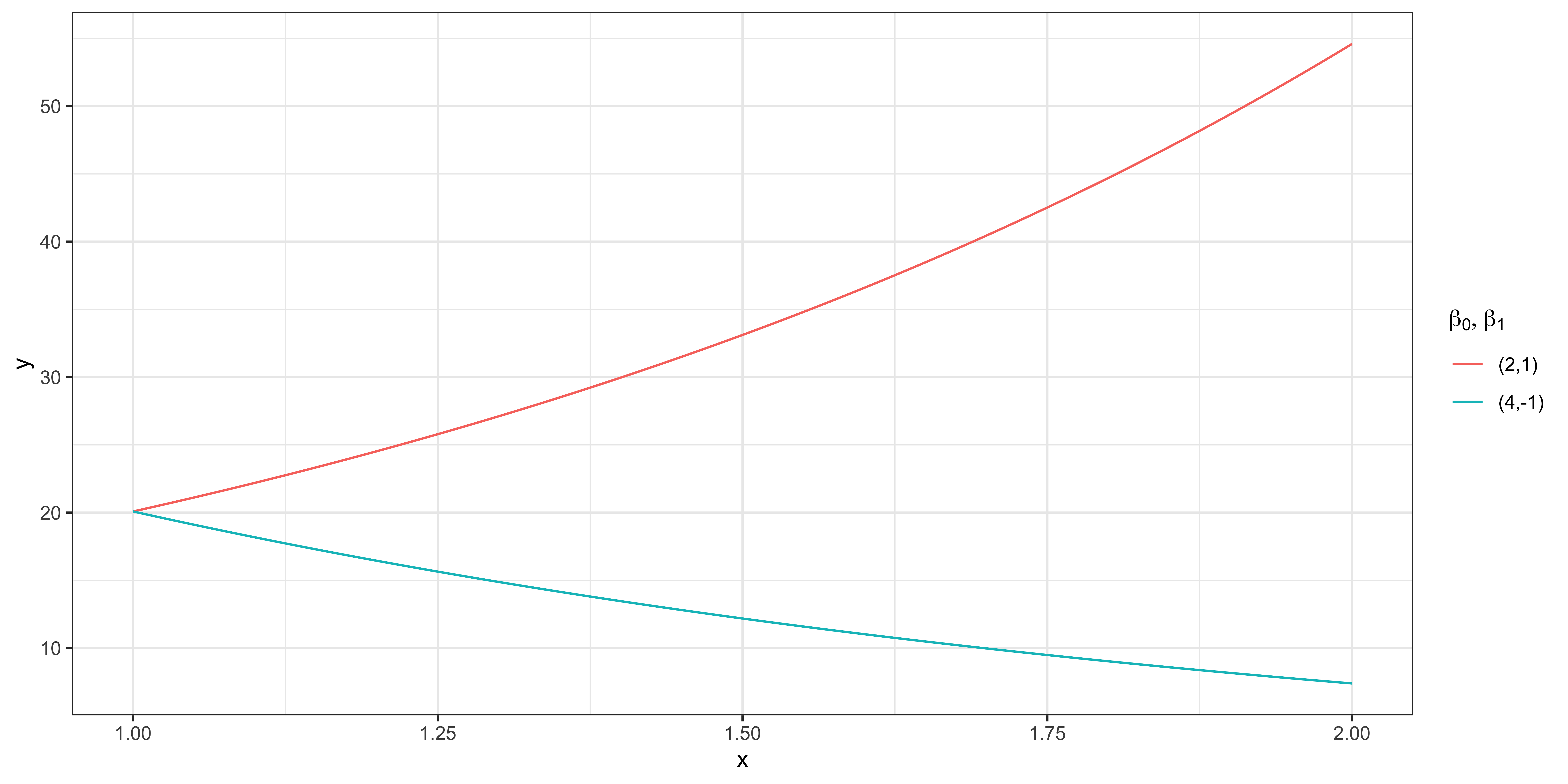
Example models

log-linear

$log(y_i)= \beta_0+\beta_1 x_i + u_i$

linear-log

$y_i= \beta_0+\beta_1 log(x_i) + u_i$

log-log

$log(y_i)= \beta_0+\beta_1 log(x_i) + u_i$

quadratic

$y_i= \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + u_i$

In the models we just saw, the dependent variable and independent variable are non-linearly related, how come are these models called simple linear model?
“linear” in simple linear model means that the model is linear in parameter , but not in variable

Examples: Non-linear models

\[\begin{align*} y_i=\beta_0+x_i^{\beta_1}+u_i \\ y_i=\frac{x_i}{\beta_0+\beta_1 x_i}+u_i \end{align*}\]

Note

Transformation of the dependent and independent variables would not affect the properties of the OLS estimator as long as the model is linear in parameter.

Consider a following model:

\[\begin{align*} \mbox{corn yield} = \beta_0 + \beta_1 \cdot \mbox{fertilizer} + \mu \end{align*}\]

Question

What is wrong with this model?

Answer

It assumes that fertilizer affects corn yield the same way no matter how much fertilizer you apply. It does not reflect the reality that the impact of fertilizer becomes almost zero at some point. A better model?

Basics
Visualization
Example
Estimated model

Model

\[\begin{align} log(y_i)= \beta_0+\beta_1 x_i + u_i \notag \end{align}\]

Calculus

Differentiating the both sides wrt $x_i$,

\[\begin{align} \frac{1}{y_i}\cdot\frac{\partial y_i}{\partial x_i} = \beta_1 \Rightarrow \frac{\Delta y_i}{y_i} = \beta_1 \Delta x_i \notag \end{align}\]

Interpretation

$\beta_1$ measures a percentage change in $y_i$ (once multiplied by 100) when $x_i$ is increased by one unit

Model

\[\begin{align} log(wage)=\beta_0 + \beta_1 educ + u \notag \end{align}\]

Calculus

Differentiating both sides with respect to $educ$,

\[\begin{align} \frac{1}{wage} \frac{\partial wage}{\partial educ} = \beta_1 \Rightarrow \frac{\Delta wage}{wage} = \beta_1\Delta educ\notag \end{align}\]

Interpretation

If education increases by 1 year $(\Delta educ=1)$, then wage increases by $\beta_1*100\%$ $(\frac{\Delta wage}{wage}=\beta_1)$

When you estimate the following model using the wage dataset:

\[log(wage)=\beta_0 + \beta_1 educ + u \notag\]

Then, the estimated equation is the following:

\[\begin{align} \widehat{log(wage)}=0.584+0.083 educ \notag \end{align}\] \[\begin{align} E[\widehat{wage}]=e^{0.584+0.083 educ} \end{align}\]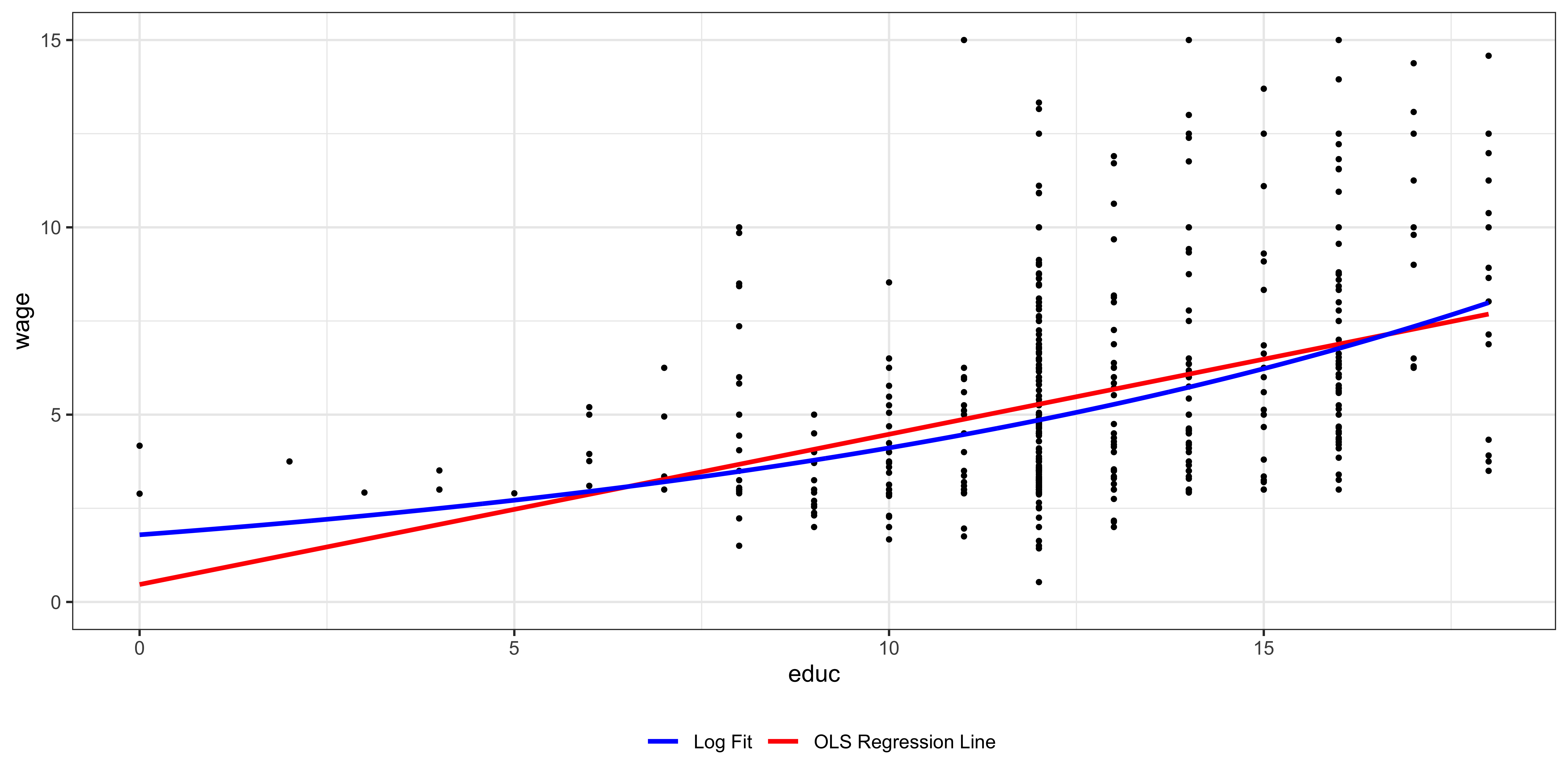

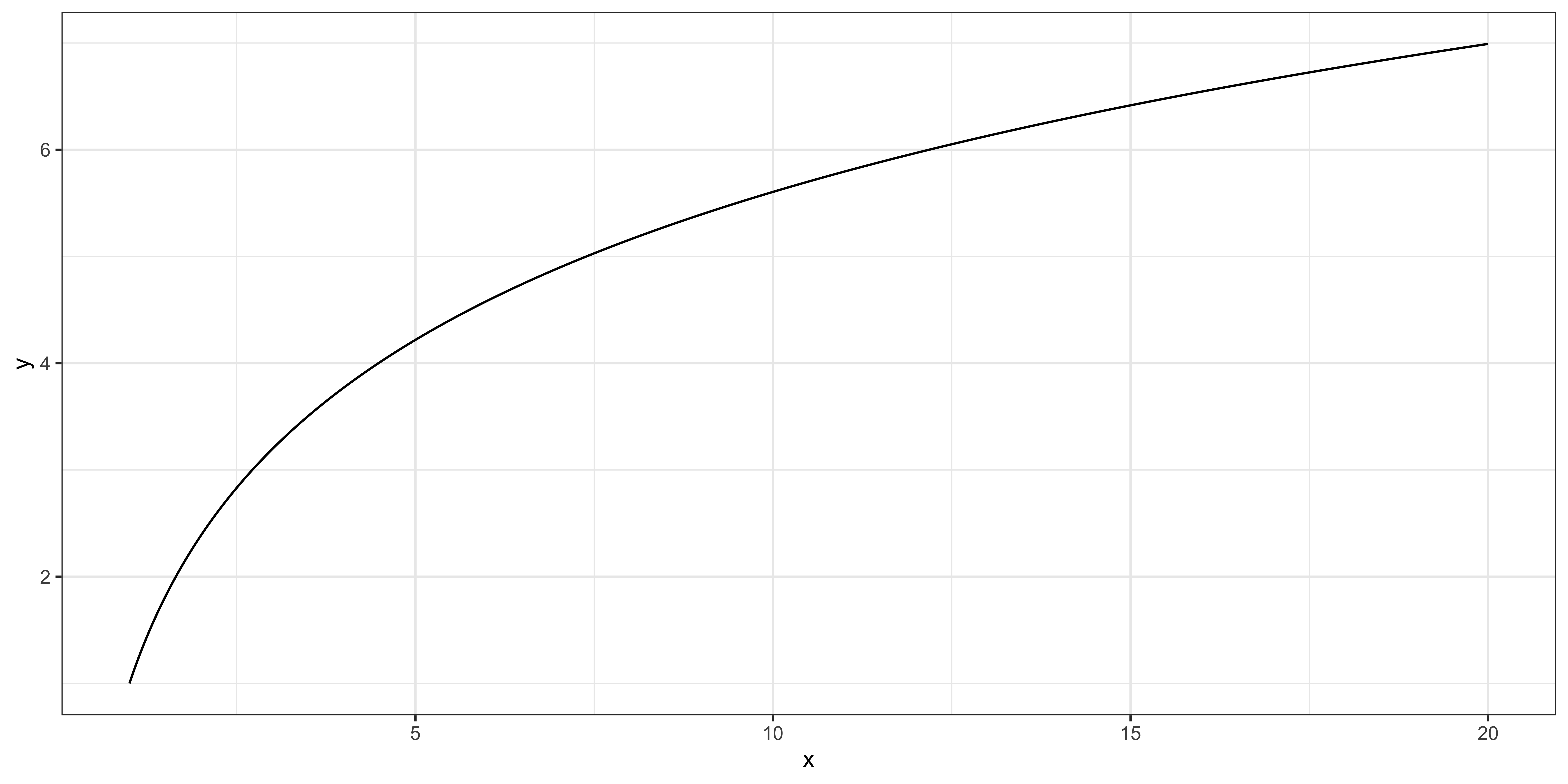
Basics
Visualization

Model

\[\begin{align} y_i= \beta_0+\beta_1 log(x_i) +u_i \notag \end{align}\]

Calculus

Differentiating the both sides wrt $x_i$,

\[\begin{align} \frac{\partial y_i}{\partial x_i} = \frac{\beta_1}{x_i} \Rightarrow \Delta y_i = \beta_1\frac{\Delta x_i}{x_i} \notag \end{align}\]

Interpretation

When $x$ increases by 0.01 ($1\%$) $y$ increases by $\beta_1 \times 0.01$.

\[y = \beta_0 + \beta_1 log(x) = 1 + 2 \times log(x)\]

Model

\[\begin{align} log(y_i)= \beta_0+\beta_1 log(x_i) +u_i \notag \end{align}\]

Calculus

Differentiating the both sides wrt $x_i$,

\[\begin{align} \frac{\partial y_i}{y_i}/\frac{\partial x_i}{x_i} = \beta_1 \Rightarrow \frac{\Delta y_i}{y_i} = \beta_1 \frac{\Delta x_i}{x_i}\notag \end{align}\]

Interpretation

A percentage change in $x$ would result in a $\beta_1$ percentage change in $y_i$ (constant elasticity)

Basics
Visualization
Example
Implementation in R
Estimated Model
Marginal impact of $educ$

Model

$y_i= \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + u_i$

Calculus

Differentiating the both sides wrt $x_i$,

$\frac{\partial y_i}{\partial x_i} = \beta_1 + 2*\beta_2 x_i\Rightarrow \Delta y_i = (\beta_1 + 2*\beta_2 x_i)\Delta x_i$

Interpretation

When $x$ increases by 1 unit $(\Delta x_i=1)$, $y$ increases by $\beta_1 + 2*\beta_2 x_i$

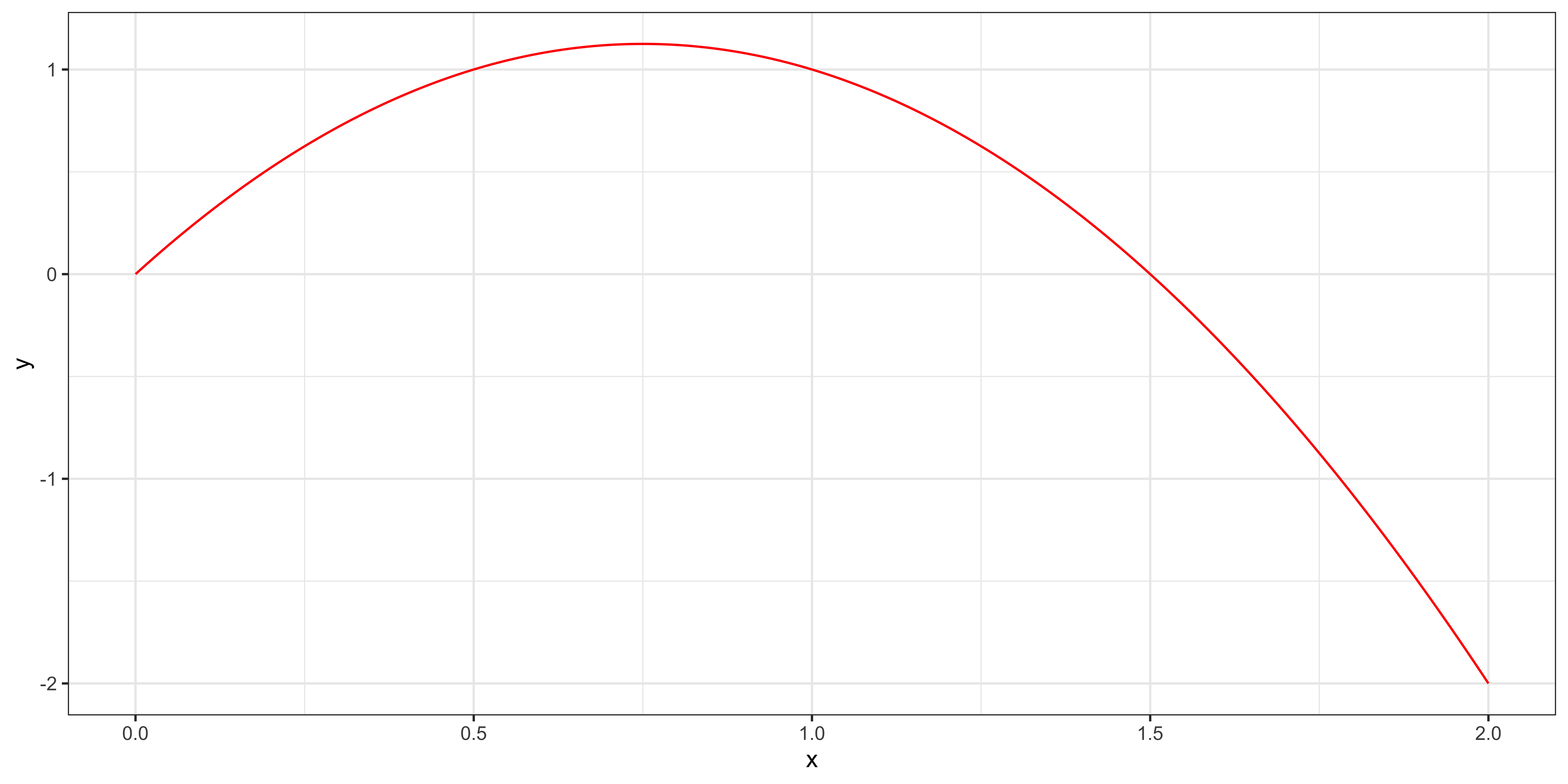
Quadratic functional form is quite flexible.

$y = x + x^2$ $(\beta_1 = 1, \beta_2 = 1)$

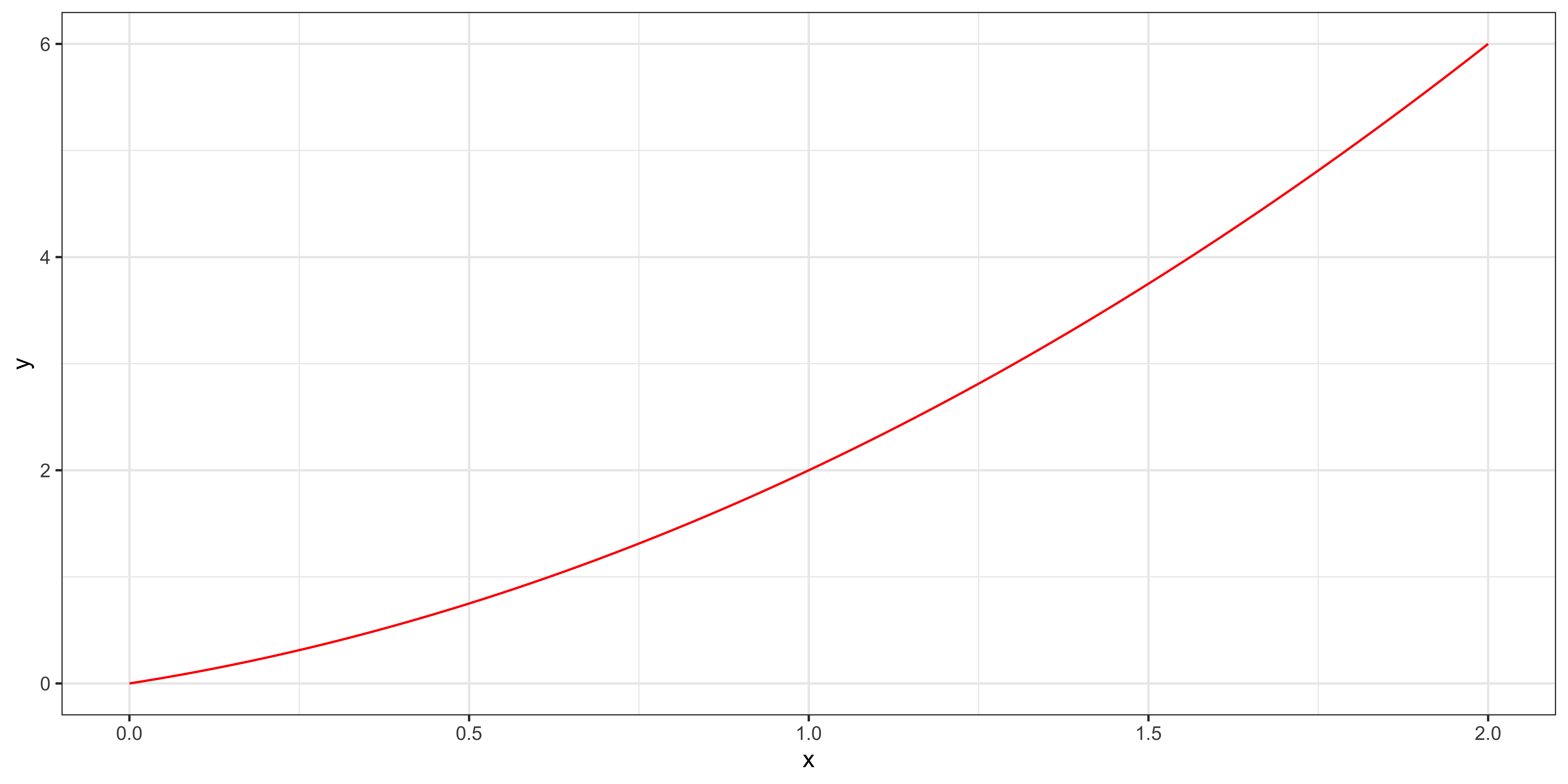
$y = 3x-2x^2$ $(\beta_1 = 3, \beta_2 = -2)$

Education impacts of income

The marginal impact of education (the impact of a small change in education on income) may differ what level of education you have had:

How much does it help to have two more years of education when you have had education until elementary school?
How much does it help to have two more years of education when you have graduated a college?
How much does it help to spend two more years as a Ph.D student if you have already spent six years in a Ph.D program

Observation

The marginal impact of education does not seem to be linear.

When you want to include a variable that is a transformation of an existing variable, you can use I() function in which you write the mathematical expression of the desired transformation.

Estimated Model

$wage = 5.60 - 2.12\times female -0.416\times educ + 0.039\times educ^2$

According to the estimated model, the marginal impact of $educ$ is:

$\frac{\partial wage}{\partial educ} = -0.416+0.039\times 2\times educ$

When $educ = 4$, additional year of education is going to increase hourly wage by -0.104 on average
When $educ = 10$, additional year of education is going to increase hourly wage by 0.364 on average

Statistical significance of the marginal impact

Marginal impcat
In the linear case
The quadratic case

Let’s work with the income model, in which the marginal impact of $educ$ is:

\[\begin{align*} \frac{\partial wage}{\partial educ} = -0.416+0.039\times 2\times educ \end{align*}\]

$\beta_{educ}$: $-0.416$ $(t$-stat $= -1.80)$
$\beta_{educ^2}$: $0.039$ $(t$-stat $= 4.10)$

Question

So, is the marginal impact of $educ$ statistically significantly different from $0$?

Model and marginal impact
Testing?

Regression

Estimated model

$wage = 0.62+0.51 \times educ$

Question 1
Question 2

What is the marginal impact of $educ$?

Answer

0.51

Does the marginal impact of education vary depending on the level of education?

Answer

No, the model we estimated assumed that the marginal impact of education is constant.

You can just test if $\hat{\beta}_{educ}$ (the marginal impact of education) is statistically significantly different from $0$, which is just a t-test.

Issue
Example 1
R implementation
Example 2
R implementation

With the quadratic specification

The marginal impact of education varies depending on your education level
There is no single test that tells you whether the marginal impact of education is statistically significant universally
Indeed, you need different tests for different values education levels

Marginal impact of education

$\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times educ$

Hypothesis testing

Does additional year of education has a statistically significant impact (positive or negative) if your current education level is 4?

$H_0$: $\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 4 =0$
$H_1$: $\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 4 \ne 0$

Question

Is this

test of a single coefficient? (t-test)
test of a single equation with multiple coefficients? (t-test)
test of multiples equations with multiple coefficients? (F-test)

t-statistic

$t = \frac{\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 4}{se(\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 4)} = \frac{\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 8}{se(\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 8)}$

Remember, a trick to do this test using R is take advantage of the fact that $F_{1, n-k-1} \sim t_{n-k-1}^2$.

Since the p-value is 0.529, we do not reject the null.

Marginal impact of education

$\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times educ$

Hypothesis testing

Does additional year of education has a statistically significant impact (positive or negative) if your current education level is 10?

$H_0$: $\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 10 =0$
$H_1$: $\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 10 \ne 0$

Question

Is this

test of a single coefficient? (t-test)
test of a single equation with multiple coefficients? (t-test)
test of multiples equations with multiple coefficients? (F-test)

t-statistic

$t = \frac{\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 10}{se(\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 2 \times 10)} = \frac{\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 20}{se(\hat{\beta}_{educ} + \hat{\beta}_{educ^2} \times 20)}$

Since the much lower than is 0.01, we can reject the null at the 1% level.

Interaction terms

What is it?
Marginal impact
R implementation
Estimated model
Hypothesis testing

A variable that is a multiplication of two variables

Example

$educ\times exper$

A model with an interaction term

$wage = \beta_0 + \beta_1 exper + \beta_2 educ \times exper + u$

Marginal impact of education:

$\frac{\partial wage}{\partial exper} = \beta_1+\beta_2\times educ$

Implications

The marginal impact of experience depends on education

$\beta_1$: the marginal impact of experience when $educ=0$
if $\beta_2>0$: additional year of experience is worth more when you have more years of education

Just like the quadratic case with $educ^2$, you can use I().

Estimated Model

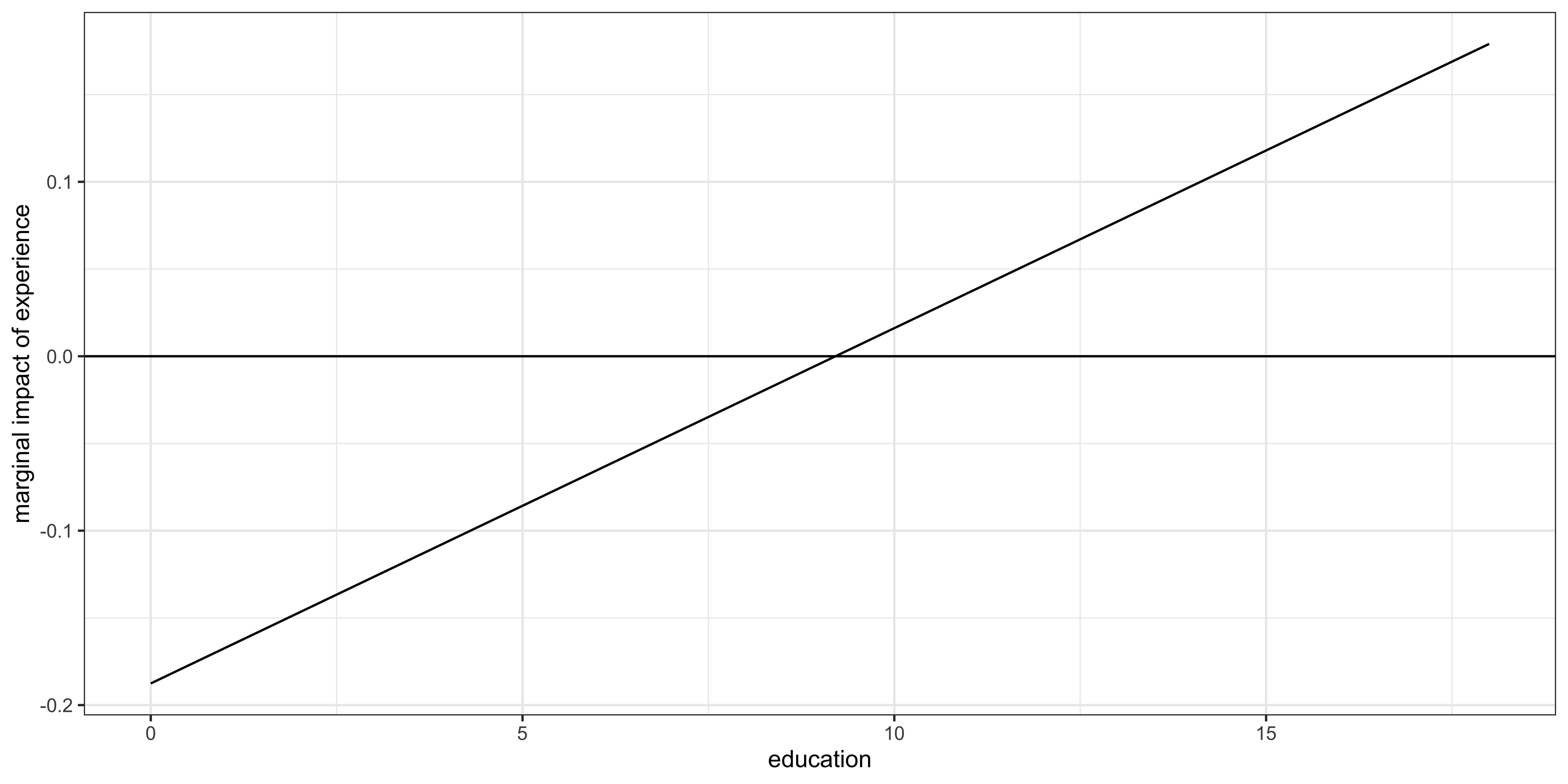
$wage = 6.121 - 2.418 \times female - 0.188 \times exper + 0.020 \times educ \times exper$

Marginal impact of experience

$\frac{\partial wage}{\partial exper} = - 0.188 + 0.020 \times educ$

Marginal impact of $exper$:

Histogram of education:

Hypothesis
R implementation

Just like the case of the quadratic specification of education, marginal impact of experience is not constant

We can test if the marginal impact of experience is statistically significant for a given level of education

When $educ=10$, $\frac{\partial wage}{\partial exper} = - 0.188 + 0.020 \times 10=0.012$
When $educ=15$, $\frac{\partial wage}{\partial exper} = - 0.188 + 0.020 \times 15=0.112$

Question

Does additional year of experience has a statistically significant impact (positive or negative) if your current education level is 10

Hypothesis

$H_0$: $\hat{\beta}_{exper} + \hat{\beta}_{exper\_educ} \times 10=0$
$H_1$: $\hat{\beta}_{exper} + \hat{\beta}_{exper\_educ} \times 10=0$

Including qualitative information

Issue
Binary variables
Use male instead?

Issue

How do we include qualitative information as an independent variable?

Examples

male or female (binary)
married or single (binary)
high-school, college, masters, or Ph.D (more than two states)

Dummy variable
Model with dummy a variable
R implementation
Visualization

Dummy variable

Relevant information in binary variables can be captured by a zero-one variable that takes the value of $1$ for one state and $0$ for the other state
We use “dummy variable” to refer to a binary (zero-one) variable

Example

Model

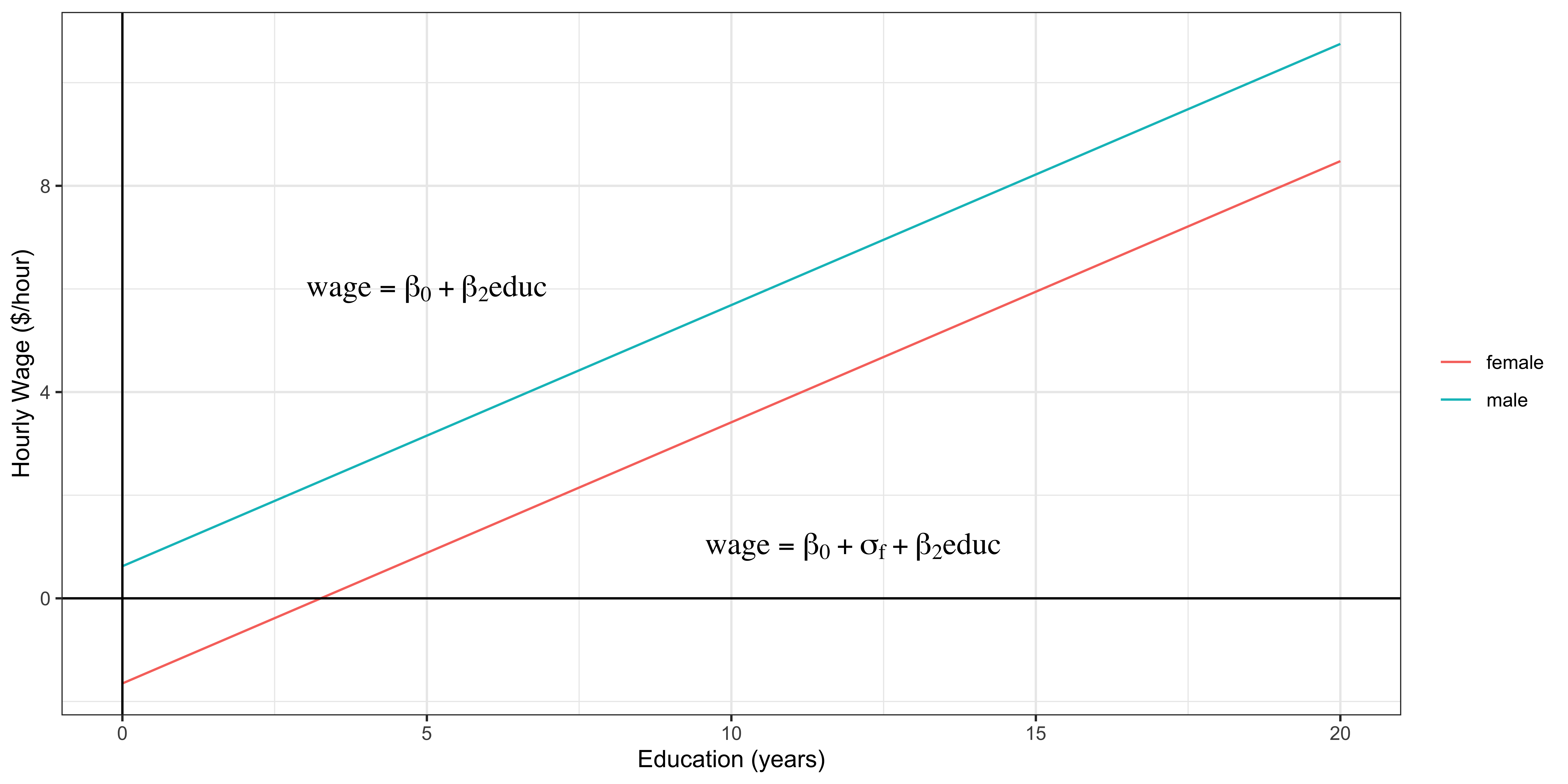
$wage = \beta_0 +\sigma_f female +\beta_2 educ + u$

Interpretation

female: $E[wage|female=1,educ] = \beta_0 + \sigma_f +\beta_2 educ$
male: $E[wage|female=0,educ] = \beta_0 + \beta_2 educ$

This means that

$\sigma_f = E[wage|female=1,educ]-E[wage|female=0,educ]$

Verbally,

$\sigma_f$ is the difference in the expected wage conditional on education between female and male
$\sigma_f$ measures how much more (less) female workers make compared to male workers ( baseline ) if they were to have the same education level

R implementation

Interpretation

Female workers make -2.2733619 ($/hour) less than male workers on average even though they have the same education level.

Model and theory
Regression results
Question
Perfect Collinearity

Model

$wage = \beta_0 +\sigma_m male +\beta_2 educ + u$

Interpretation

male: $E[wage|male = 1,educ] = \beta_0 + \sigma_m +\beta_2 educ$
female: $E[wage|male = 0,educ] = \beta_0 + \beta_2 educ$

This means that

$\sigma_m = E[wage|male=1,educ]-E[wage|male=0,educ]$

Verbally,

$\sigma_m$ is the difference in the expected wage conditional on education between female and male
$\sigma_m$ measures how much more (less) male workers make compared to female workers (baseline) if they were to have the same education level

Important

Whichever status that is given the value of $0$ becomes the baseline

Regression results

Interpretation

Male workers make NA ($/hour) more than female workers on average even though they have the same education level.

What do you think will happen if we include both male and female dummy variables?

Answer

They contain redundant information
Indeed, including both of them along with the intercept would cause perfect collinearity problem
So, you need to drop either one of them

In the model, $intercept = male + female$, which causes perfec collinearity.

Here is what happens if you include both:

One of the variables that cause perfect collinearity is automatically dropped.

Interactions with a dummy variable

Issue
Example using R
Interpretation

In the previous example, the impact of education on wage was modeled to be exactly the same
Can we build a more flexible model that allows us to estimate the differential impacts of education on wage between male and female?

A more flexible model

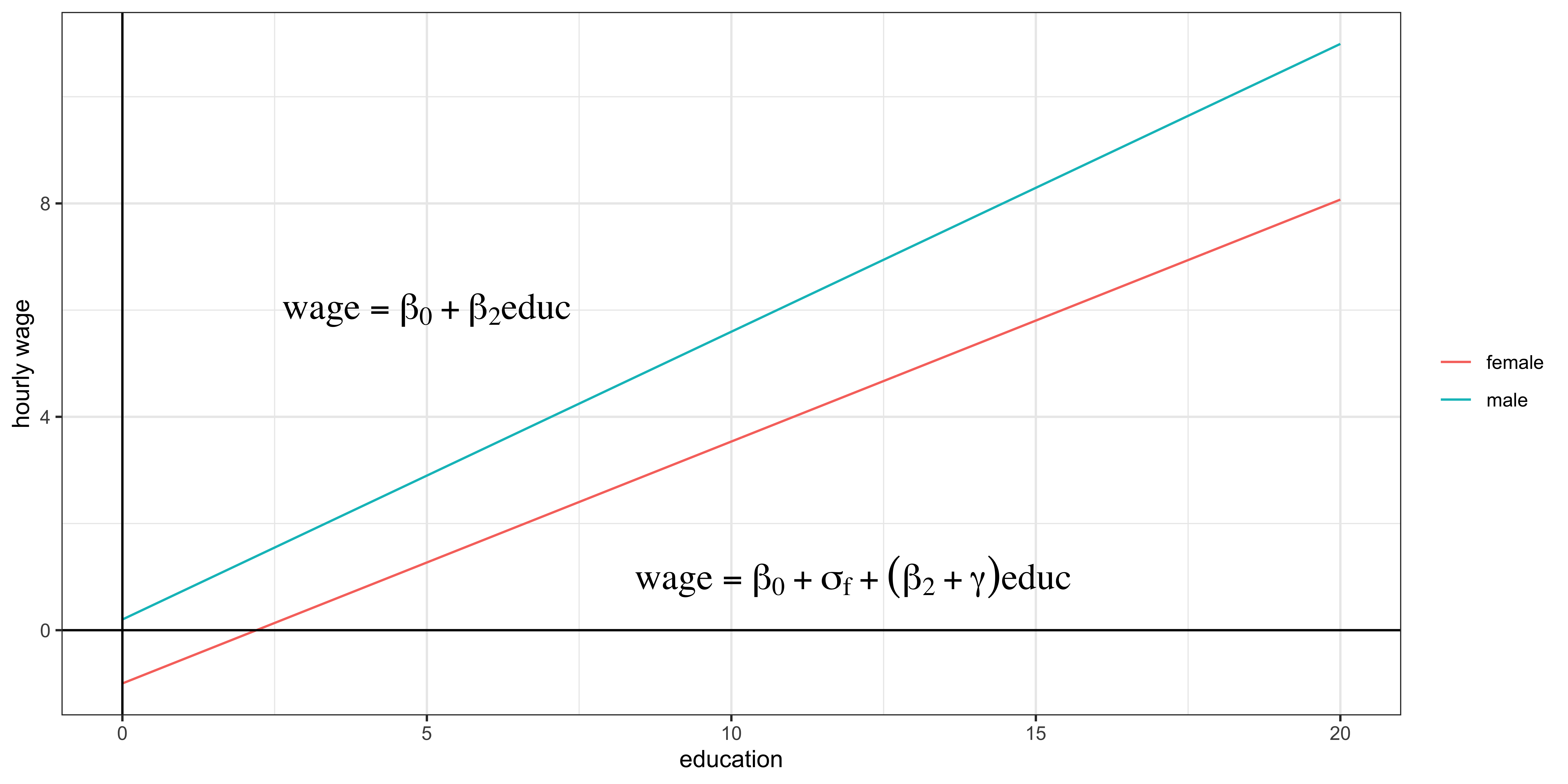
$wage = \beta_0 + \sigma_f female +\beta_2 educ + \gamma female\times educ + u$

female: $E[wage|female=1,educ] = \beta_0 + \sigma_f +(\beta_2+\gamma) educ$
male: $E[wage|female=0,educ] = \beta_0 + \beta_2 educ$

Interpretation

For female, education is more effective by $\gamma$ than it is for male.

The marginal benefit of education is 0.086 ($/hour) less for females workers than for male workers on average.

Categorical variable: more than two states

Issue
Model

Consider a variable called $degree$ which has three status values: college, master, and doctor.
Unlike a binary variable, there are three status values.
How do we include a categorical variable like this in a model?

What do we do about this?

You can create three dummy variables likes below:

college: 1 if the highest degree is college, 0 otherwise
master: 1 if the highest degree is Master’s, 0 otherwise
doctor: 1 if the highest degree is Ph.D., 0 otherwise

You then include two (the number of status values - 1) of the three dummy variables:

Model

$wage = \beta_0 + \sigma_m master +\sigma_d doctor + \beta_1 educ + u$

$college$: $E[wage|master=0, doctor = 0, educ] = \beta_0 + \beta_1 educ$
$master$: $E[wage|master=1, doctor = 0, educ] = \beta_0 + \sigma_m + \beta_1 educ$
$doctor$: $E[wage|master=0, doctor = 1, educ] = \beta_0 + \sigma_d + \beta_1 educ$

Interpretation

$\sigma_m$: the impact of having a MS degree relative to having a college degree

$\sigma_d$: the impact of having a Ph.D. degree relative to having a college degree

Important

The omitted category (here, college) becomes the baseline.

Structural differences across groups

Definition
What to do?
Interpretation
R code
What do you see?
Test of joint significance

Structural difference refers to the fundamental differences in the model of a phenomenon in the population:

Example

Male: $cumgpa = \alpha_0 + \alpha_1 sat + \alpha_2 hsperc + \alpha_3 tothrs + u$

Female: $cumgpa = \beta_0 + \beta_1 sat + \beta_2 hsperc + \beta_3 tothrs + u$

$cumgpa$: college grade points averages for male and female college athletes
$sat$: SAT score
$hsperc$: high school rank percentile
$tothrs$: total hours of college courses

In this example,

$cumgpa$ are determined in a fundamentally different manner between female and male students.

You do not want to run a single regression that fits a single model for both female and male students.

If you suspect that the underlying process of how the dependent variable is determined vary across groups, then you should test that hypothesis!

To do so,

You estimate the model that allows to estimate separate models across groups within a single regression analysis.

A more flexible model

\[cumgpa = \beta_0 + \sigma_0 female + \beta_1 sat + \sigma_1 (sat \times female)\] \[\;\; + \beta_2 hsperc + \sigma_2 (hsperc \times female)\] \[\qquad + \beta_3 tothrs + \sigma_3 (tothrs \times female) + u\]

Male: $E[cumgpa] = \beta_0 + \beta_1 sat + \beta_2 hsperc + \beta_3 tothrs$ Female: $E[cumgpa] = (\beta_0 +\sigma_0) + (\beta_1+\sigma_1) sat + (\beta_2+\sigma_2) hsperc + (\beta_3+\sigma_3) tothrs$

Interpretation

$\beta$s are commonly shared by female and male students
$\sigma$s capture the differences between female and male students

Null Hypothesis

(verbally) The model of GPA for male and female students are not structurally different.
(mathematically) $H_0: \;\; \sigma_0=0,\;\; \sigma_1=0, \;\; \sigma_2=0, \;\; \mbox{and} \;\; \sigma_3=0$

Question

What test do we do? t-test or F-test?

Answer

F-test.

Run the unrestricted model with all the interaction terms:

Regression results

What do you see?

None of the variables that involve $female$ are statistically significant at the 5% level individually.
Does this mean that $male$ and $female$ students have the same regression function?
No, we are testing the joint significance of the coefficients. We need to do an $F$-test!

R coding tips: categorical variables and interaction terms

Prepare a dataset
Data
i()
Interactions terms

Take a look at the data,

You can use the i() function inside fixest::feols() like below:

ref = "Indiana U" sets the base category to "Indiana U".

So, for example, the highlighted line means that faculty members at Michigan State U make $9,118$ USD less annually than those at Indiana U.

Key

You do not have to make bunch of dummy variables like the original dataset. Just use i(catergory_variable).

You can use i() for creating interactions of a categorical variable and a continuous variable.

Suppose you are interested in understanding the impact of pubindx (continuous) by university (categorical), then

So, the marginal impact of pubindex is $436$ greater for those at Michigan State U than those at Indiana U.

07: Econometric Modeling

Functional form

Functional form

Various functional forms

Statistical significance of the marginal impact

Statistical significance of the marginal impact

Interaction terms

Interaction terms

Including qualitative information

Including qualitative information

Interactions with a dummy variable

Interactions with a dummy variable

Categorical variable: more than two states

Structural differences across groups

R coding tips: categorical variables and interaction terms

Other miscellaneous topic

Goodness of fit: \(R^2\)

Scaling