06: Standard Error Estimation

Heteroskedasticity

---

Homoskedasticity and Heteroskedasticity

• Review
• Visualization
• Central Questions
• Coefficient estimators
• Variance of the coefficient estimators

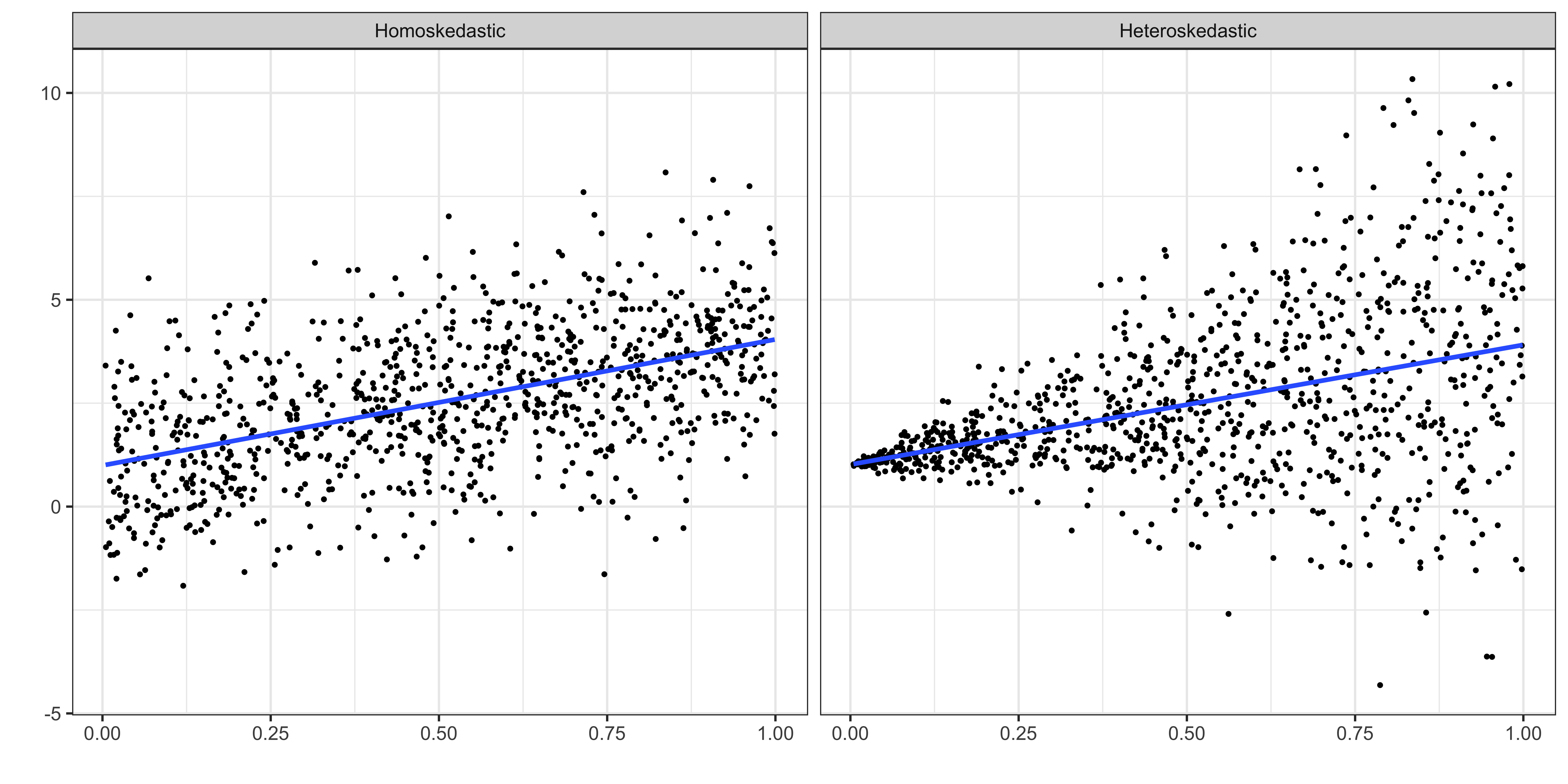
Homoskedasticity

\(Var(u|x) = \sigma^2\)

Heteroskedasticity

\(Var(u|x) = f(x)\)

What are the consequences of assuming the error is homoskedastic when it is heteroskedastic in reality?

• Estimation of coefficients \((\widehat{\beta}_j)\)?
• Estimation of the variance of \(\widehat{\beta}_j\)?

• Question
• Answer

Are OLS estimators unbiased when error is heteroskedastic?

Yes. We do not need to use the homoskedasticity assumption to prove that the OLS estimator is unbiased.

• homeskedastic error
• heteroskedastic error
• Consequences

We learned that when the homoskedasticity assumption holds, then,

\(Var(\widehat{\beta}_j) = \frac{\sigma^2}{SST_x(1-R^2_j)}\)

We used the following as the estimator of \(Var(\widehat{\beta}_j)\)

\(\frac{\widehat{\sigma}^2}{SST_x(1-R^2_j)}\) where \(\widehat{\sigma}^2 = \frac{\sum_{i=1}^{N} \widehat{u}_i^2}{N-k-1}\)

Important

By default , R and other statistical software uses this formula to get estimates of the variance of \(\widehat{\beta}_j\).

But, under heteroskedasticity,

\(Var(\widehat{\beta}_j) \ne \frac{\sigma^2}{SST_x(1-R^2_j)}\)

• Question
• Answer

Is \(E[\widehat{Var(\widehat{\beta}_j)}_{default}] \equiv E\Big[\frac{\widehat{\sigma}^2}{SST_x(1-R^2_j)}\Big]=Var(\widehat{\beta}_j)\) under heteroskedasticity?

No.

So, what are the consequences of using \(\widehat{Var(\widehat{\beta}_j)}=\frac{\widehat{\sigma}^2}{SST_x(1-R^2_j)}\) under heteroskedasticity?

\(\;\;\;\;\downarrow\)

Your hypothesis testing is going to be biased!!

• Question
• Answer

What does it mean to have hypothesis testing biased?

Roughly speaking, it means that you over-reject/under-reject the hypothesis than you intend to.

Consequence of heteroskedasticity on testing

• Motivation and setup
• MC simulation

Let’s run MC simulations to see the consequence of ignoring heteroskedasticity.

Model

\(y = 1 + \beta x + u\), where \(\beta = 0\)

Test of interest

• \(H_0:\) \(\beta=0\)
• \(H_1:\) \(\beta \ne 0\)

• Question
• Answer

If you test the null hypothesis at the \(5\%\) significance level, what should be the probability that you reject the null hypothesis when it is actually true?

\(Pr(\mbox{reject} \;\; H_0|H_0 \;\; \mbox{is true})=?\)

\(5\%\)

• conceptual steps
• R implementation
• Results

• generate a dataset so that \(\beta_1\) (the coefficient on \(x\)) is zero

\[y=\beta_0+\beta_1 x + v\]

• estimate the model and find \(\widehat{\beta}_1\) and \(\widehat{se(\widehat{\beta}_1)}\)
• calculate \(t\)-statistic \((\widehat{\beta}_x-0)/\widehat{se(\widehat{\beta}_x)}\) and decide whether you reject the null or not
• repeat the above 1000 times
• check how often you reject the null (should be close to 50 times)

Consequence of ignoring heteroskedasticity

We rejected the null hypothesis 10.8% of the time, instead of \(5\%\).

• So, in this case, you are more likely to claim that \(x\) has a statistically significant impact than you are supposed to.

• The use of the formula \(\frac{\widehat{\sigma}^2}{SST_x(1-R^2_j)}\) seemed to (over/under)-estimate the true variance of the OLS estimators?

• In general, the direction of bias is ambiguous.

How should we address this problem?

• What to do?
• Robust estimator of se
• In practice

Now, we understand the consequence of heteroskedasticity:

\(\frac{\widehat{\sigma}^2}{SST_x(1-R^2_j)}\) is a biased estimator of \(Var(\widehat{\beta})\), which makes any kind of testings based on it invalid.

Can we credibly estimate the variance of the OLS estimators?

White-Huber-Eicker heteroskedasticity-robust standard error estimator

• valid in the presence of heteroskedasticity of unknown form
• heteroskedasticity-robust standard error estimator in short

Heteroskedasticity-robust standard error estimator

\(\widehat{Var(\widehat{\beta}_j)} = \frac{\sum_{i=1}^n \widehat{r}^2_{i,j} \widehat{u}^2_i}{SSR^2_j}\)

• \(\widehat{u}_i\): residual from regressing \(y\) on all the independent variables
• \(\widehat{r}_{i,j}\): residual from regressing \(x_j\) on all other independent variables for \(i\)th observation
• \(SSR^2_j\): the sum of squared residuals from regressing \(x_j\) on all other independent variables

Note

We spend NO time to try to understand what’s going on with the estimator.

What you need is

• understand the consequence of heteroskedasticity
• know there is an estimator that is appropriate under heteroskedasticity, meaning that it will give you the correct estimate of the variance of the OLS estimator
• know how to use the heteroskedasticity-robust standard error estimator in practice using \(R\) (or some other software)

Here is the well-accepted procedure in econometric analysis:

• Estimate the model using OLS (you do nothing special here)

• Assume the error term is heteroskedastic and estimate the variance of the OLS estimators

  • There are tests to whether error is heteroskedastic or not: Breusch-Pagan test and White test
  • In practice, almost nobody bothers to conduct these tests
  • We do not learn how to run these tests

• Replace the estimates from \(\widehat{Var(\widehat{\beta})}_{default}\) with those from \(\widehat{Var(\widehat{\beta})}_{robust}\) for testing

• But, we do not replace coefficient estimates (remember, coefficient estimation is still unbiased under heteroskedasticity)

Robust standard error estimation in R

• Implementation in R
• Reporting the regression results
• Alternatively (Recommended)
• Validation

• Preparation
• Obtaining Heteroskedasticity-robust SE estimates
• Compare with the Default

Let’s run a regression using MLB1.dta.

We use

• the stats::vcov() function to estimate heteroskedasticity-robust standard errors

• the fixest::se() function from the fixest package to estimate heteroskedasticity-robust standard errors (you can always get SE from VCOV)

• the summary() function to do tests of \(\beta_j = 0\)

General Syntax

Here is the general syntax to obtain various types of VCOV (and se) esimaties:

#* vcov
vcov(regression result, vcov = "type of vcov")

#* only the standard errors
fixest::se(regression result, vcov = "type of vcov")

heteroskedasticity-robust standard error estimation

Specifically for White-Huber heteroskedasticity-robust VCOV and se estimates,

Default

Heteroskedasticity-robust

In presenting the regression results in a nicely formatted table, we used modelsummary::msummary().

We can easily swap the default se with the heteroskedasticity-robust se using the statistic_override option in msummary().

vcov_het <- vcov(reg_mlb, vcov = "hetero")
vcov_homo <- vcov(reg_mlb)

modelsummary::msummary(
  list(reg_mlb, reg_mlb),
  statistic_override = list(vcov_het, vcov_homo),
  # keep these options as they are
  stars = TRUE,
  gof_omit = "IC|Log|Adj|F|Pseudo|Within"
) 

	(1)	(2)
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)	11.042***	11.042***
	(0.343)	(0.343)
years	0.166***	0.166***
	(0.013)	(0.013)
bavg	0.005***	0.005***
	(0.001)	(0.001)
Num.Obs.	353	353
R2	0.367	0.367
RMSE	0.94	0.94
Std.Errors	IID	IID

Alternatively, you could add the vcov option like below inside fixest::feols(). Then, you do not need statistic_override option to override the default VCOV estimates.

reg_mlb_with_rvcov <- 
  fixest::feols(
    log(salary) ~ years + bavg,
    vcov = "hetero", 
    data = mlb1
  ) 

modelsummary::msummary(
  list(reg_mlb_with_rvcov),
  # keep these options as they are
  stars = TRUE,
  gof_omit = "IC|Log|Adj|F|Pseudo|Within"
) 

	(1)
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
(Intercept)	11.042***
	(0.704)
years	0.166***
	(0.018)
bavg	0.005+
	(0.003)
Num.Obs.	353
R2	0.367
RMSE	0.94
Std.Errors	Heteroskedasticity-robust

• MC simulation
• MC simulation results

Does the heteroskedasticity-robust se estimator really work? Let’s see using MC simulations:

Okay, not perfect. But, certainly better.

Clustered Error

---

Clustered Error

• What is it?
• Consequences of clustered error
• MC simulations
• What to do?
• In practice

• Often times, observations can be grouped into clusters
• Errors within the cluster can be correlated

• Example 1
• Example 2

College GPA: cluster by college

\(GPA_{col} = \beta_0 + \beta_1 income + \beta_2 GPA_{hs} + u\)

• Your observations consist of students’ GPA scores across many colleges
• Because of some unobserved (omitted) school characteristics, error terms for the individuals in the same college might be correlated.
  • grading policy

Eduction Impacts on Income: cluster by individual

• Your observations consist of 500 individuals with each individual tracked over 10 years

• Because of some unobserved (omitted) individual characteristics, error terms for time-series observations within an individual might be correlated.

  • innate ability

• Question 1
• Question 2
• Question 3

Are the OLS estimators of the coefficients biased in the presence of clustered error?

Answer

No, the correlation between \(x\) and \(u\) would hurt you, but not correlation among \(u\).

Are \(\widehat{Var(\widehat{\beta})}_{default}\) unbiased estimators of \(Var(\widehat{\beta})\)?

Answer

No, \(\widehat{Var(\widehat{\beta})}_{default}\) is unbiased only under homoskedasticity assumption, which assumes no correlation between errors.

Which has more information?

• two errors that are independent
• two errors that are correlated

Consequences

• If you were to use \(\widehat{Var(\widehat{\beta})}_{default}\) to estimate \(Var(\widehat{\beta})\) in the presence of clustered error, you would (under/over)-estimate the true \(Var(\widehat{\beta})\).

• This would lead to rejecting null hypothesis (more/less) often than you are supposed to.

• Conceptual steps
• Data Generating Process (R)
• Visualization of clustered error
• MC simulation (R)
• Results

Here are the conceptual steps of the MC simulations to see the consequence of clustered error.

• generate data according to the generating process in which the error terms \((u)\) within the cluster (two clusters in this example) is correlated and \(\beta_1\) is set to 0 in the model below:

\[ \begin{aligned} y = \beta_0 + \beta_1 x + u \end{aligned} \]

• estimate the model and find \(\widehat{\beta}_x\) and \(\widehat{se(\widehat{\beta}_x)}\)
• calculate \(t\)-statistic \((\widehat{\beta}_x/\widehat{se(\widehat{\beta}_x)})\) for the (correct) null hypothesis of \(\beta_1 = 0\)
• repeat steps 1-3 for 1000 times
• see how many times out of 1000 times you reject the null hypothesis: \(H_0:\) \(\beta_x=0\)

Important

• clustered error can severely bias your test results
• it tends to make the impact of explanatory variables more significant than they truly are because the default estimator of the variance of the OLS estimator tends to greatly under-estimate the true variance of the OLS estimator.

• Cluster-robust SE estimation
• R implementation
• R Demonstration
• Compare
• Alternatively (Recommended)

There exist estimators of \(Var(\widehat{\beta})\) that take into account the possibility that errors are clustered.

• We call such estimators cluster-robust variance covariance estimator denoted as \((\widehat{Var(\widehat{\beta})}_{cl})\)

• We call standart error estimates from such estimators cluster-robust standard error estimates

I neither derive nor show the mathematical expressions of these estimators.

This is what you need to do

• understand the consequence of clustered errors

• know there are estimators that are appropriate under clustered error

• know that the estimators we will learn take care of heteroskedasticity at the same time (so, they really are cluster- and heteroskedasticity-robust standard error estimators)

• know how to use the estimators in \(R\) (or some other software)

Cluster-robust standard error

Similar with the vcov option for White-Huber heteroskedasticity-robust se, we can use the cluster option to get cluster-robust se.

Before an R demonstration

Let’s take a look at the MLB data again.

• nl: the group variable we cluster around (1 if in the National league, 0 if in the American league).

Step 1

Run a regression

Step 2

Apply vcov() or se() with the cluster = option.

Default

Cluster-robust standard error

Or, you could add the cluster option inside fixest::feols().

Syntax

fixes::feols(y ~ x, cluster = ~ variable to cluster by, data = data)

Example

This code cluster by nl.

Just like the heteroskedasticity-present case before,

• Estimate the model using OLS (you do nothing special here)

• Assume the error term is clustered and/or heteroskedastic, and estimate the variance of the OLS estimators \((Var(\widehat{\beta}))\) using cluster-robust standard error estimators

• Replace the estimates from \(\widehat{Var(\widehat{\beta})}_{default}\) with those from \(\widehat{Var(\widehat{\beta})}_{cl}\) for testing

• But, we do not replace coefficient estimates.

But does it really work?

Let’s run MC simulations to see if the use of the cluster-robust standard error estimation method works

• MC simulation (R)
• MC simulation results
• More groups
• MC simulation results

Well, we are still rejecting too often than we should, but it is much better than the default VCOV estimator that rejected 74% of the time.

Important

• Cluster-robust standard error estimation gets better as the number of groups gets larger
• The number of groups of 2 is too small (the MLB case)
• As a rule of thumb, # of groups larger than 50 is sufficiently large, but we just saw we still over-rejected the null of \(\beta = 0\) three times more than we should.

Better. But, we are still over-rejecting. Don’t forget it is certainly better than using the default!