05: Hypothesis Testing
Review on Statistical Hypothesis Testing
Hypothesis Testing
Here is the general step of any hypothesis testing:
Step 1: specify the null \((H_0)\) and alternative \((H_1)\) hypotheses
Step 2: find the distribution of the test statistic if the null hypothesis is true
Step 3: calculate the test statistic based on the data and regression results
Step 4: define the significance level
Step 5: check how unlikely that you get the actual test statistic (found at Step 3) if indeed the null hypothesis is true
Goal
Suppose you want to test if the expected value of a normally distributed random variable \((x)\) is 1 or not.
State of Knowledge
We do know \(x\) follows a normal distribution and its variance is 4 for some reason.
Your Estimator
Your estimator is the sample mean: \(\theta = \sum_{i=1}^J x_i/J\)
Math Aside 1
\(Var(ax) = a^2 Var(X)\)
So, we know that \(\theta \sim N(\alpha, 4/J)\) (of course \(\alpha\) is not known).
Math Aside 2
If \(x \sim N(a, b)\), then, \(x-a \sim N(0, b)\) (shift)
So, \(\frac{x-a}{\sqrt{b}} \sim N(0, 1)\) (combined with Math Aside 1)
This means,
Since \(\theta = \sum_{i=1}^J x_i/J\) and \(x_i \sim N(\alpha, 4)\),
- \(Var(\theta) = J \times \frac{1}{J^2}Var(x) = 4/J\)
- \(\frac{\sqrt{J}}{2} \cdot (\theta - \alpha)\sim N(0, 1)\).
We established that \(\frac{\sqrt{J}}{2} \cdot (\theta - \alpha)\sim N(0, 1)\).
The null hypothesis is \(\alpha = 1\).
If \(\alpha = 1\) is indeed true, then \(\sqrt{J} \times (\theta - 1)/2 \sim N(0, 1)\).
In other words, if you multiply the sample mean by the square root of the number of observations and divide it by 2, then it follows the standard normal distribution like below.
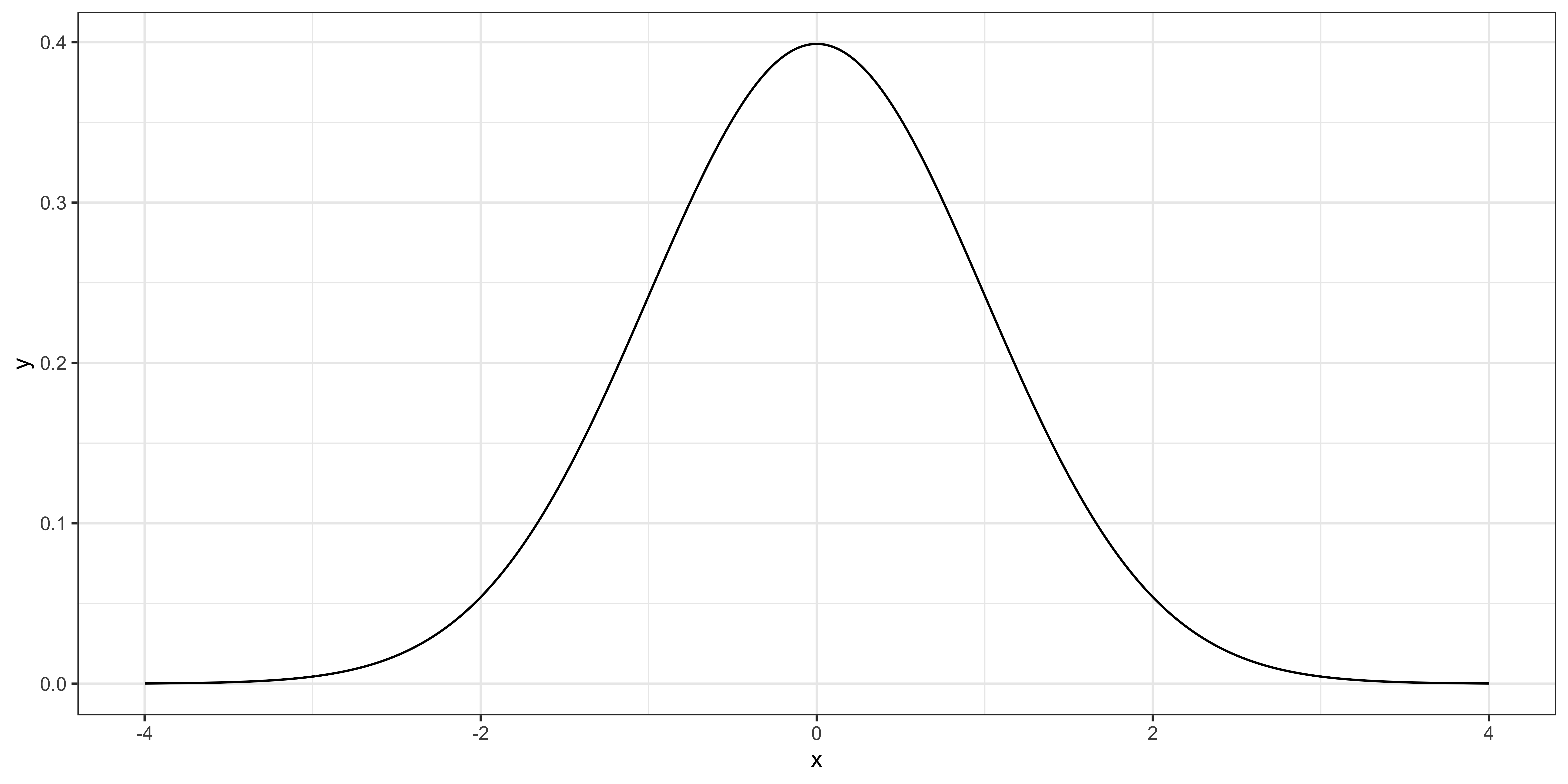
Suppose you have obtained 100 samples \((J = 100)\) and calculated \(\theta\) (sample mean), which turned out to be 2.
Then, your test statistic is \(\sqrt{100} \times (2-1)/2 = 5\).
How unlikely is it to get the number you got (5) if the null hypothesis is indeed true?
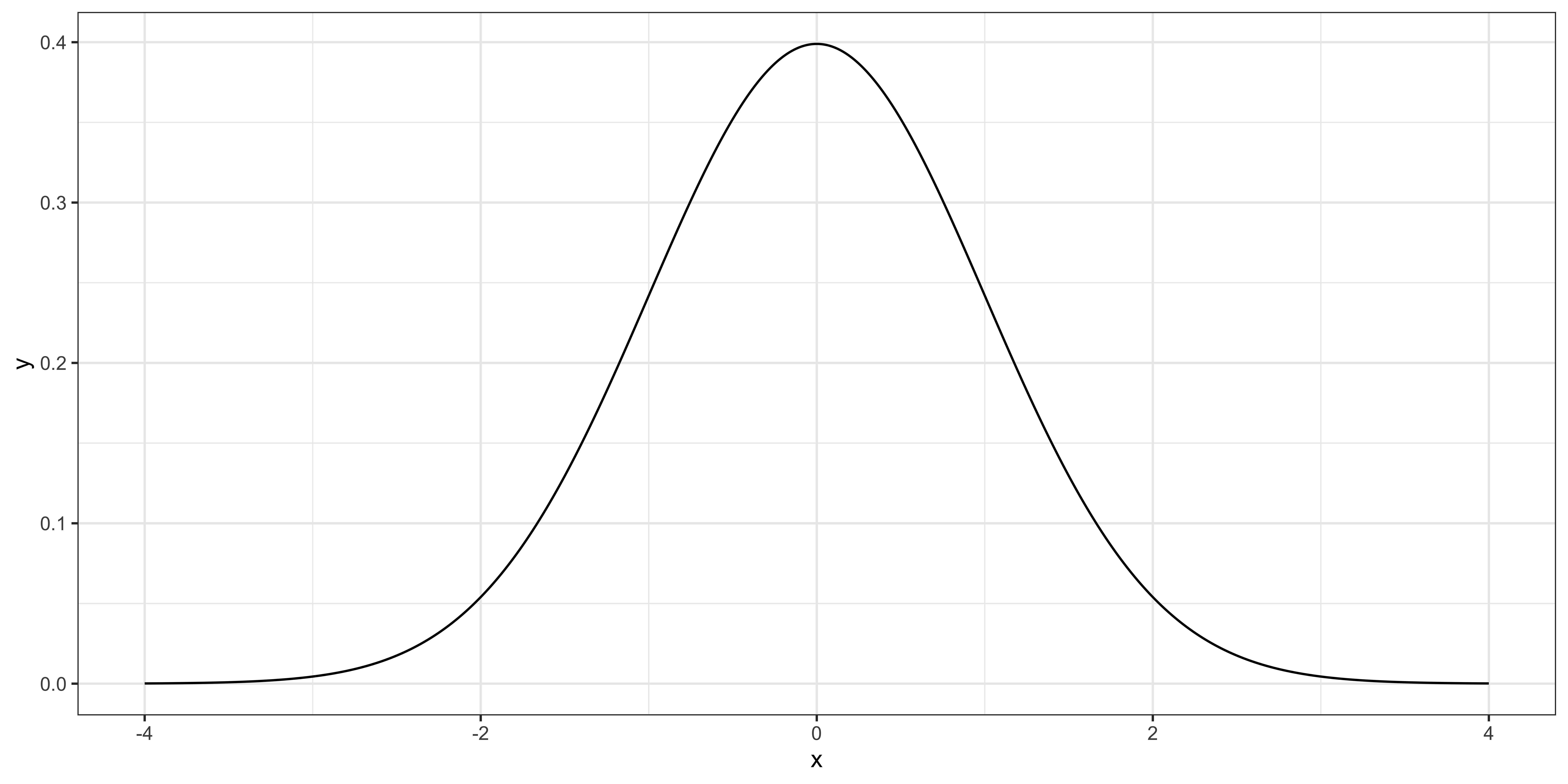
Suppose you have obtained 400 samples \((J = 400)\) and calculated \(\theta\) (sample mean), which turned out to be 1.02.
Then, your test statistic is \(\sqrt{400} \times (1.02-1)/2 = 0.2\).
How unlikely is it to get the number you got (0.2) if the null hypothesis is indeed true?
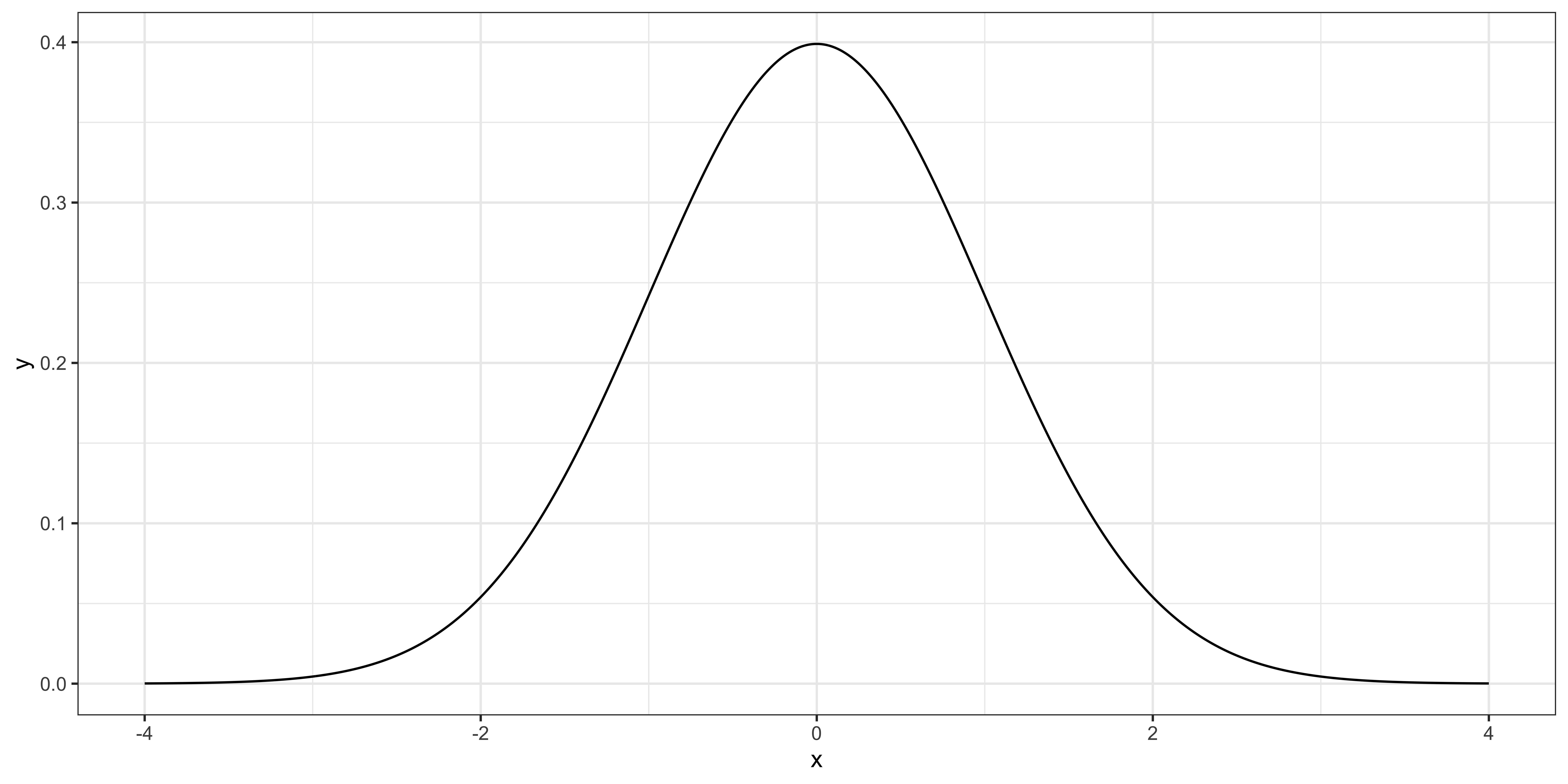
Note that you do not really need to use \(\sqrt{J} \times (\theta - \alpha)/2\) as your test statistic.
You could alternatively use \(\theta - \alpha\). But, in that case, you need to be looking at \(N(0, 4/J)\) instead of \(N(0, 1)\) to see how unlikely you get the number you got.
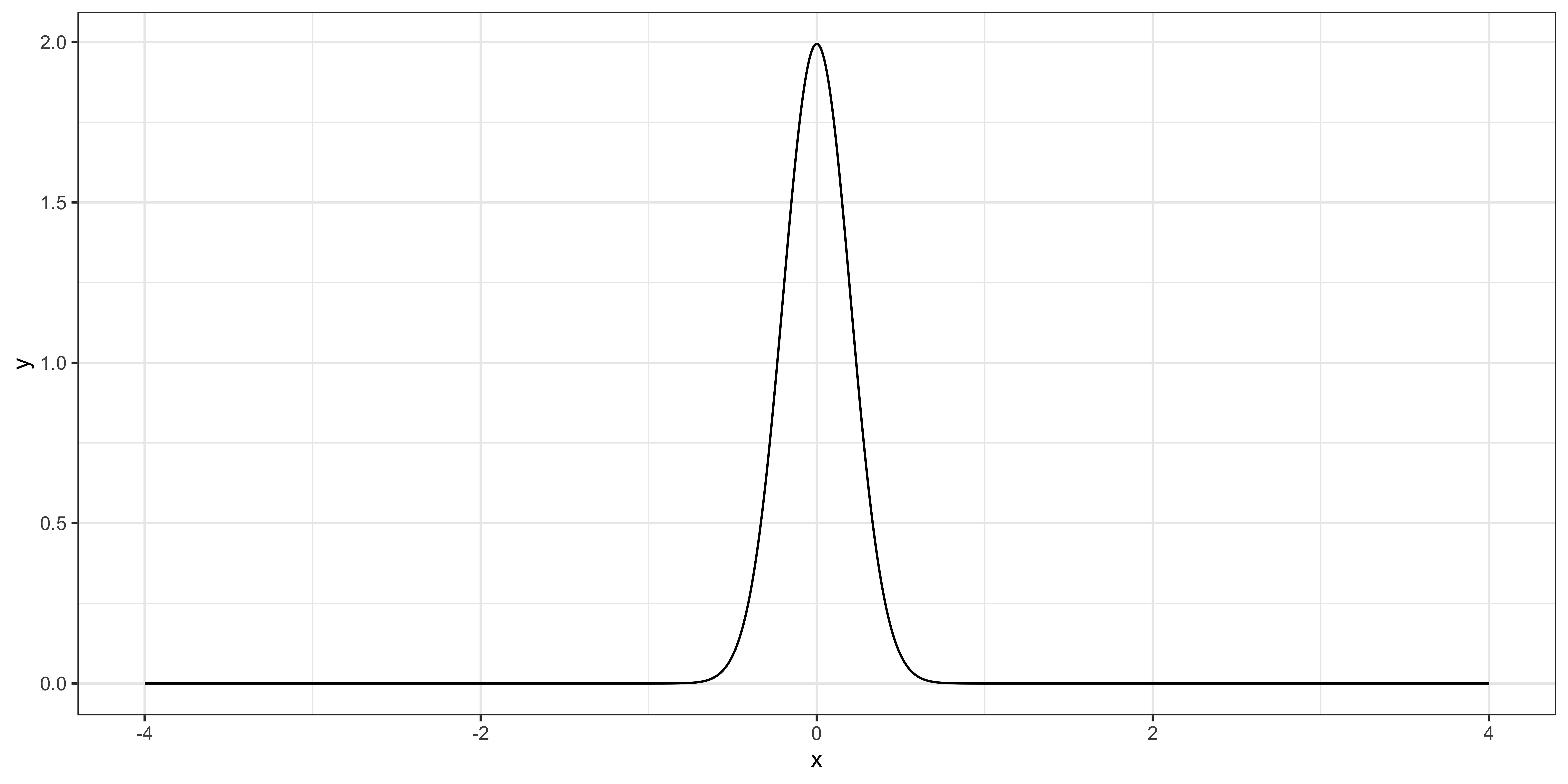
For example, when the number of observations is 100 \((J = 100)\), the distribution of \(\theta-\alpha\) looks like the figure on the right.
Reconsider the case 1
Suppose you have obtained 100 samples \((J = 100)\) and calculated \(\theta\) (sample mean), which turned out to be 2.
Then, your test statistic is \(2-1 = 1\).
Is it unlikely for you to get 1 if the null hypothesis is true?
The conclusion would be exactly the same as using \(\sqrt{J} \times (\theta - \alpha)/2\) because the distribution under the null is adjusted according to the test statistic you use.
Note
We always use normalize test statistic so that we can always look up the same distribution.
What do we need?
- test-statistic of which we know the distribution (e.g., t-distribution, Normal distribution) assuming the null hypothesis
What do we (often) do?
- transform (most of the time) a raw random variable (e.g., sample mean in the example above) into a test statistic of which we know the distribution assuming that the null hypothesis is true
- e.g., we transformed the sample mean so that it follows the standard Normal distribution.
- check if the actual number you got from the test statistic is likely to happen or not (formal criteria has not been discussed yet)
You have collected data on annual salary for those who graduated from University A and B. You are interested in testing whether the difference in annual salary between the universities (call it \(x\)) is 10 on average. You know (for unknown reasons) know that the difference is distributed as \(N(\alpha, 16)\).
- What is the null hypothesis?
- Under the null hypothesis, what is the distribution of the sample mean when the number of observation is 400?
- Normalize the test statistic so that the transformed version follows \(N(0, 1)\).
- The actual difference you observed is 10.2. What is the probability that you observe a number greater than 10.2 if the null hypothesis is true? Use
prnom().
Note
In reality,
- we need to find out what the distribution of the test statistic is
- we need to formerly define when we accept or not accept the null hypothesis
- \(\alpha = 10\)
- \(\theta \sim N(\alpha, 16/400)\)
- \(\sqrt{\frac{400}{16}}\cdot (\theta - \alpha)\)
- The test statistic is \(5 \times (10.2 - 10) = 1\)
Hypothesis Testing on the Coefficients
Hypothesis Testing of the Coefficients
Consider the following model,
\[wage = \beta_0 + \beta_1 educ + \beta_2 exper + u\]
Example Hypotheses
- education has no impact on wage \((\beta_1=0)\)
- experience has a positive impact on wage \((\beta_2>0)\)
If \(\widehat{\beta}_1\) is non-random, but just a scalar, all you have to do is just check if \(\widehat{\beta}_1=0\) or not
But, the estimate you get is just one realization of the range of values \(\widehat{\beta}_1\) could take because it is a random variable
This means that even if \(\beta_1=0\) in the population, it is possible to get an estimate that is very far from 0
So far, we learned that:
- OLS estimators are unbiased under MLR.1 ~ MLR.4
- Variance of the OLS estimator of \(\beta_j\) is \(\frac{\sigma^2}{SST_x\cdot (1-R^2_j)}\) under MLR.1 ~ MLR.5
We have NOT made any assumptions about the distribution of the error term!!
In order to perform hypothesis testing, we need to make assumptions about the distribution of error term (this is not strictly true, but more on this later)
For the purpose of hypothesis testing, we will make the following assumption:
Normality of the error term
The population error \(u\) is independent of the explanatory variables \(x_1,\dots,x_k\) and is normally distributed with zero mean and variance \(\sigma^2\):
\[u\sim N(0,\sigma^2)\]
Note
The normality assumption is much more than error term being distributed as Normal.
Independence of the error term implies
- \(E[u|x] = 0\)
- \(Var[u|x]= \sigma^2\)
So, we are necessarily assuming MLR.4 and MLR.5 hold by the independence assumption.
distribution of the dependent variable
The distribution of \(y\) conditional on \(x\) is a Normal distribution
\(y|x \sim N(\beta_0+\beta_1 x_1+\dots+\beta_k x_k,\sigma^2)\)
- \(E[y|x]\) is \(\beta_0+\beta_1 x_1+\dots+\beta_k x_k\)
- \(u|x\) is \(N(0,\sigma^2)\)
distribution of the OLS estimator
If the MLR.1 through MLR.6 are satisfied, \(OLS\) estimators are also Normally distributed!
\(\widehat{\beta}_j \sim N(\beta_j,Var(\widehat{\beta}_j))\)
which means,
\(\frac{\widehat{\beta}_j-\beta_j}{se(\widehat{\beta}_j)} \sim N(0,1)\)
Question
Okay, so are we going to use this for testing involving \(\beta_j\)?
In practice, we need to estimate \(se(\beta_j)\). If we use \(\widehat{se(\widehat{\beta}_j)}\) instead of \(se(\widehat{\beta}_j)\), then,
\(\frac{\widehat{\beta}_j-\beta_j}{\widehat{se(\widehat{\beta}_j)}} \sim t_{n-k-1}\)
where \(n-k-1\) is the degree of freedom of residual.
(Note: \(\widehat{se(\widehat{\beta}_j)} = \widehat{\sigma}^2/\big[SST_X\cdot (1-R_j^2)\big]\))
- \(k\): the number of explanatory variables included except the intercept
- \(\sigma^2\): the true variance of the error term
- \(\widehat{\sigma^2}\): the estimator (estimate) of the variance of the error term
- \(\widehat{\sigma^2} = \frac{\sum \widehat{u}_i^2}{n-k-1}\)
- \(SST_X = \sum (x_i - \bar{x})^2\)
- \(\widehat{\beta}_j\): OLS estimator (estimate) on explanatory variable \(x_j\)
- \(\widehat{\beta} = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{SST_X}\) (for simple univariate regression)
- \(var(\widehat{\beta}_j)\): the true variance of \(\widehat{\beta}_j\)
- \(R^2_j\): \(R^2\) when you regres \(x_j\) on all the other covariates (mathematical expression omitted)
- \(\widehat{var(\widehat{\beta}_j)}\): Estimator (estimate) of \(var(\widehat{\beta}_j)\)
- \(\widehat{var(\widehat{\beta}_j)} = \frac{\widehat{\sigma^2}}{SST_X\cdot(1-R^2_j)}\)
- \(se(\widehat{\beta}_j)\): square root of \(var(\widehat{\beta}_j)\)
- \(\widehat{se(\widehat{\beta}_j)}\): square root of \(\widehat{var(\widehat{\beta}_j)}\)
Details of hypothesis testing on \(\beta_j\)
Statistical hypothesis testing involves two hypotheses: Null and Alternative hypotheses.
Pretend that you are an attorney who indicted a defendant who you think committed a crime.
Null Hypothesis
Hypothesis that you would like to reject (defendant is not guilty)
Alternative Hypothesis
Hypothesis you are in support of (defendant is guilty)
one-sided alternative
\(H_0:\) \(\beta_j = 0\) \(H_1:\) \(\beta_j > 0\)
You look at the positive end of the t-distribution to see if the t-statistic you obtained is more extreme than the level of error you accept (significance level).
two-sided alternative
\(H_0:\) \(\beta_j = 0\) \(H_1:\) \(\beta_j \ne 0\)
You look at the both ends of the t-distribution to see if the t-statistic you obtained is more extreme than the level of error you accept (significance level).
Definition
The probability of rejecting the null when the null is actually true (The probability that you wrongly claim that the null hypothesis is wrong even though it’s true in reality: Type I error)
The lower the significance level, you are more sure that the null is indeed wrong when you reject the null hypothesis
Figure on the right presents the distribution of \(\frac{\widehat{\beta}_j-\beta_j}{\widehat{se(\widehat{\beta}_j)}}\) if \(\beta_j = 0\) (the null hypothesis is true).
The probability that you get a value larger than 1.66 is 5% (0.05 in area).
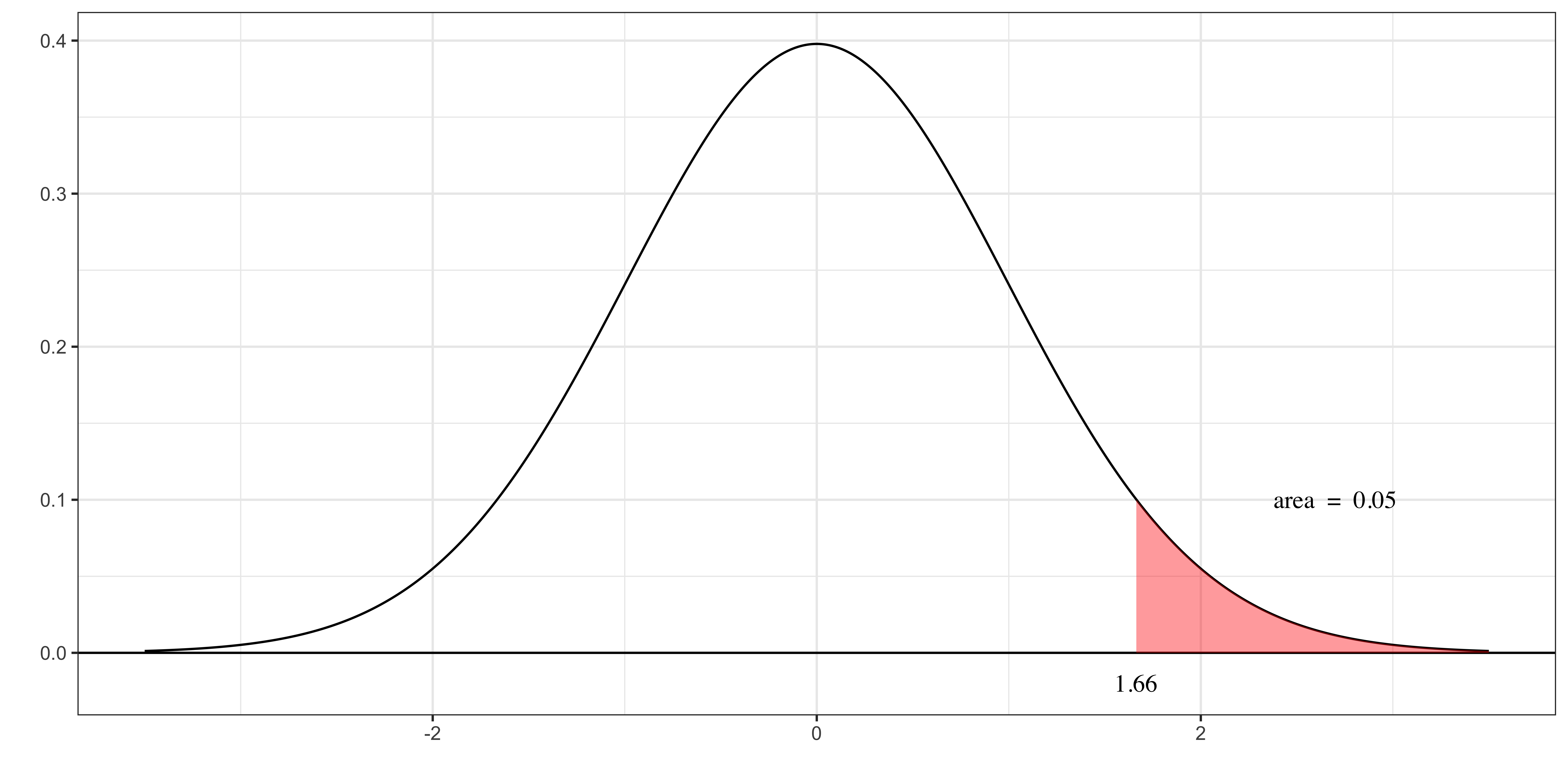
Decision Rule
Reject the null hypothesis if the t-statistic is greater than 1.66 (95% quantile of the t-distribution)
If you follow the decision rule, then you have a 5% chance that you are wrong in rejecting the null hypothesis of \(\beta_j = 0\). Here,
- 5% is the significance level
- 1.66 is the critical value above which you will reject the null
- The figure on the right presents the distribution of \(\frac{\widehat{\beta}_j-\beta_j}{\widehat{se(\widehat{\beta}_j)}}\) if \(\beta_j = 0\) (the null hypothesis is true).
- The probability that you get a value larger than 2.37 is 1% (0.01 in area).
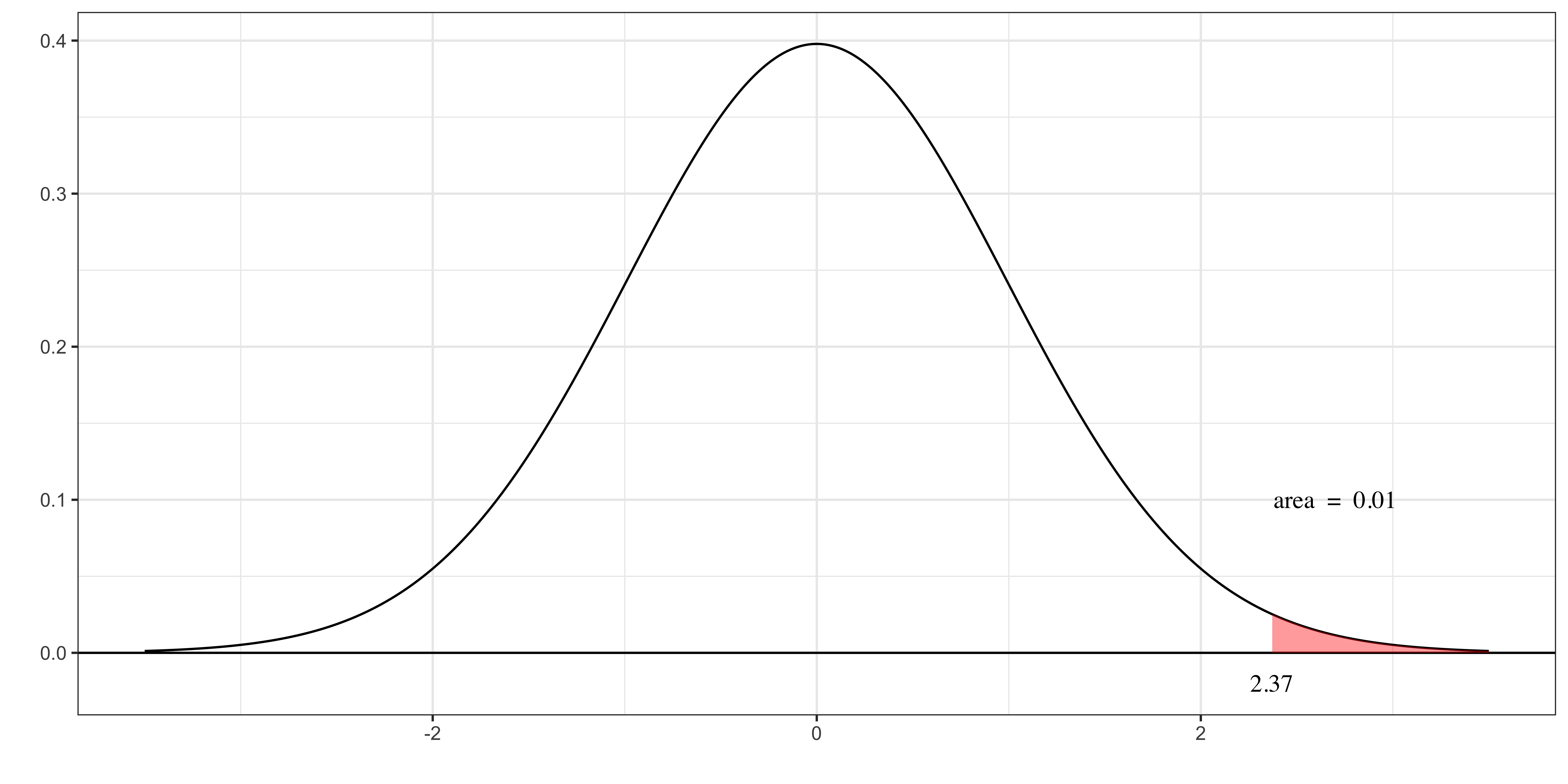
Decision Rule
Reject the null hypothesis if the t-statistic is greater than 2.37 (99% quantile of the t-distribution)
If you follow the decision rule, then you have a 1% chance that you are wrong in rejecting the null hypothesis of \(\beta_j = 0\). Here,
- 1% is the significance level
- 2.37 is the critical value above which you will reject the null
The figure on the right presents the distribution of \(\frac{\widehat{\beta}_j-\beta_j}{\widehat{se(\widehat{\beta}_j)}}\) if \(\beta_j = 0\) (the null hypothesis is true).
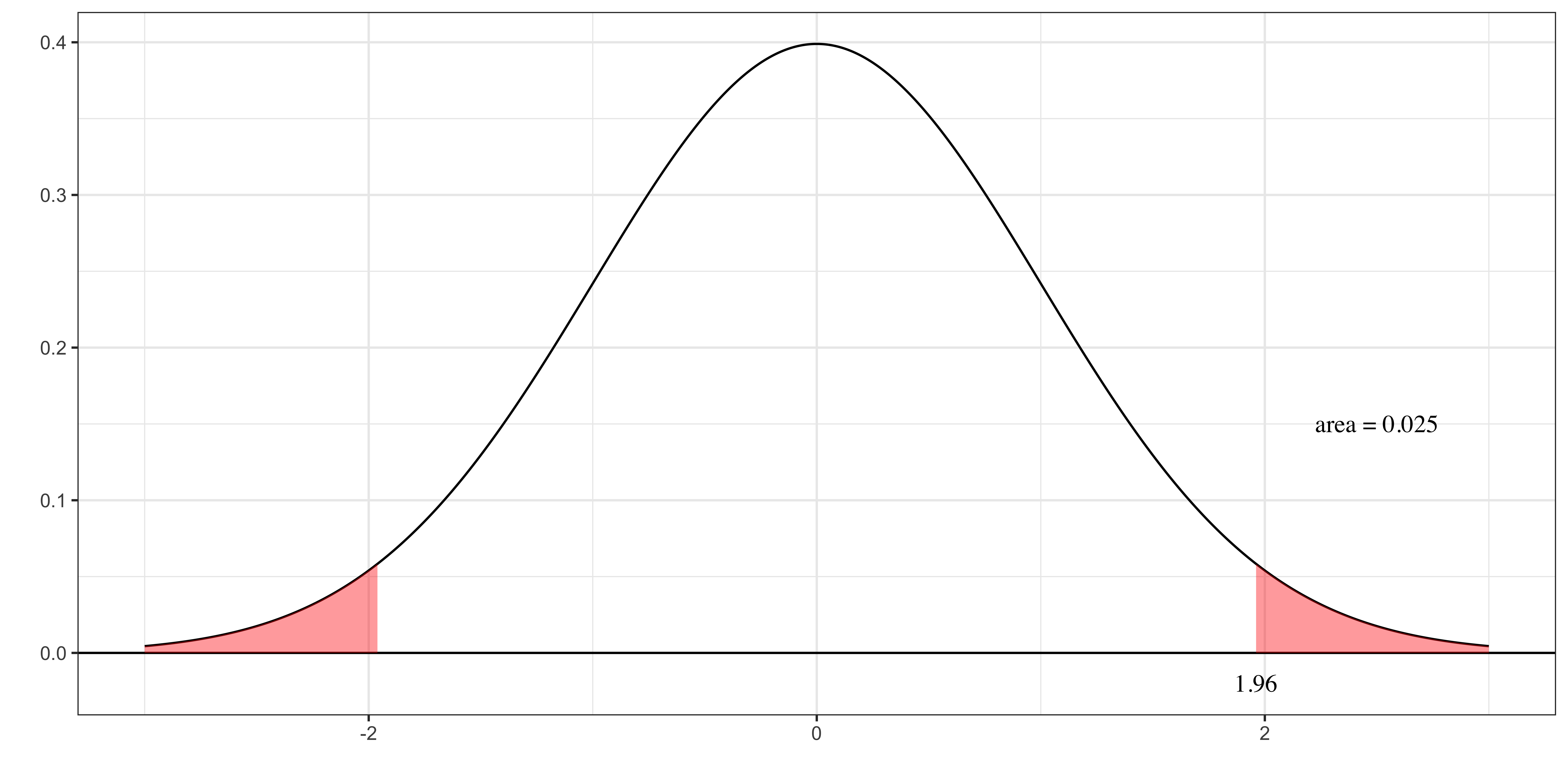
The probability that you get a value more extreme than 1.96 or -1.96 is 5% (0.05 in area cobining the two area at the edges).
(Note: irrespective of the type of tests, the distribution of t-statistics is the same.)
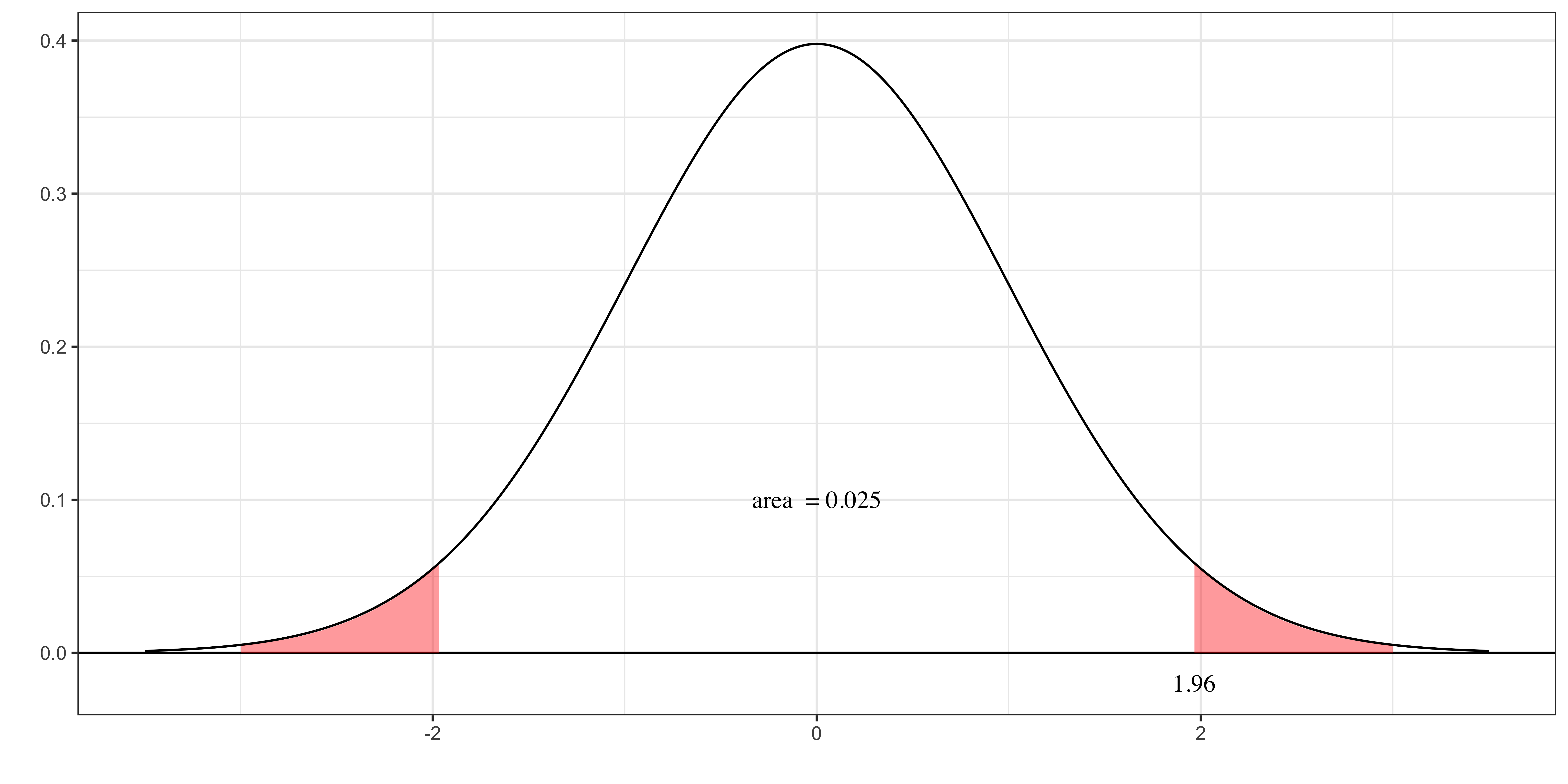
Decision Rule
Reject the null hypothesis if the absolute value of the t-statistic is greater than 1.96.
If you follow the decision rule, then you have a 5% chance that you are wrong in rejecting the null hypothesis of \(\beta_j = 0\). Here,
- 5% is the significance level
- 1.96 is the critical value above which you will reject the null
Definition
The smallest significance level at which the null hypothesis would be rejected (the probability of observing a test statistic at least as extreme as we did if the null hypothesis is true)
Suppose the t-statistic you got is 2.16. Then, there’s a 3.1% chance you reject the null when it is actually true, if you use it as the critical value.
So, the lower significance level the null hypothesis is rejected is 3.1%, which is the definition of p-value.
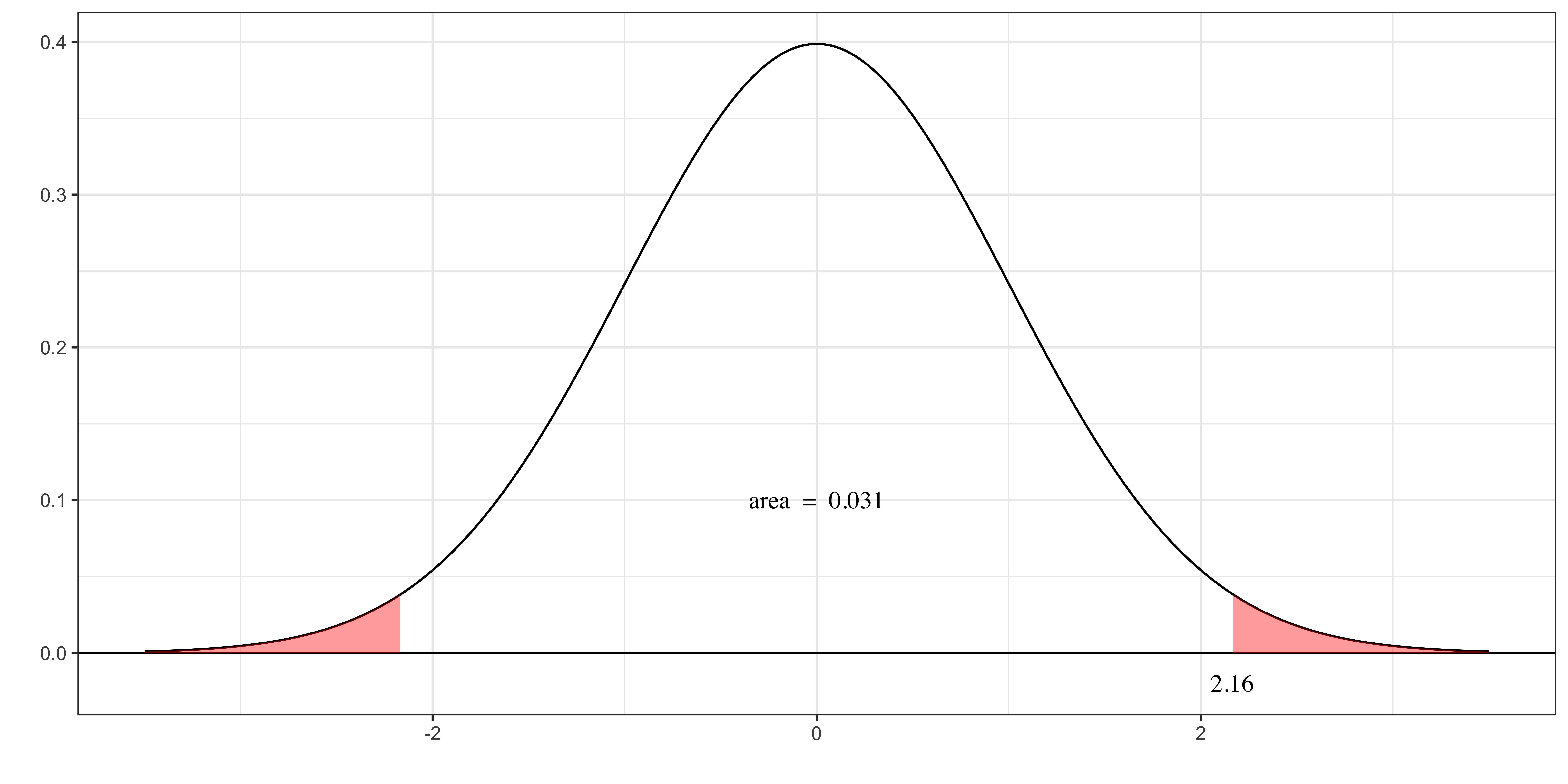
Decision rule
If the p-value is lower than your choice of significance level, then you reject the null.
This decision rule of course results in the same test results as the one we saw that uses a t-value and critical value.
Estimated Model
The impact of experience on wage:
- \(log(wage) = 0.284+0.092\times educ+0.0041\times exper + 0.022 \times tenure\)
- \(\widehat{se(\widehat{\beta}_{exper})} = 0.0017\)
- \(n = 526\)
Hypothesis
- \(H_0\): \(\beta_{exper}=0\)
- \(H_1\): \(\beta_{exper}>0\)
Test
t-statistic \(= 0.0041/0.0017 = 2.41\)
The critical value is the 99% quantile of \(t_{526-3-1}\), which is \(2.33\) (it can be obtained by qt(0.95, 522))
Since \(2.41 > 2.33\), we reject the null in favor of the alternative hypothesis at the 1% level.
R implementation
You can apply the broom::tidy() function from the broom package to access the regression results (reg_wage here) as a tibble (data.frame).
estimate: coefficient estimates \((\widehat{\beta}_j)\)std.error: \(\widehat{se(\widehat{\beta}_j}\))statistic: t-statistic for the null of \(\beta_j = 0\)p.value: p-value (for the two sided test with the null of \(\beta_j = 0\))
So, for the t-test of of \(\beta_j = 0\) is already there. You do not need to do anything further.
For the null hypothesis other than \(\beta_j = 0\), you need further work.
Suppose you are testing the null hypothesis of \(\beta_{educ} = 1\) against the alternative hypothesis of \(\beta_{educ} \ne 1\) (so, this is a two-sided test).
The t-value for this test is not available from the summary.
The degree of freedom \((n-k-1)\) of the t-distribution can be obtained by applying degrees_freedom(reg_wage, "resid"):
You can get the 97.5% quantile of the \(t_{522}\) using the qt() function:
Since the absolute value of the t-value (-7.8199528) is greater than the critical value (1.9645189), you reject the null.
Confidence Interval (CI)
Confidence Interval (CI)
Definition
If you calculate the 95% confidence interval on multiple different samples, 95% of the time, the calculated CI includes the true parameter
What confidence interval is not
The probability that a realized CI calculated from specific sample data includes the true parameter
For the assumed distribution of statistic \(x\), the \(A\%\) confidence interval of \(x\) is the range with
- lower bound: 100 − A/2 percent quantile of \(x\)
- upper bound: 100-(100 − A)/2 percent quantile of \(x\)
For the 95% CI (A = 95),
- lower bound: 2.5 (100 − 95/2) percent quantile of \(x\)
- upper bound: 97.5 (100-(100 − 95)/2) percent quantile of \(x\)
If \(x\) follows the standard normal distribution \((x \sim N(0, 1))\), then,the 2.5% and 97.5% quantiles are -1.96 and 1.96, respectively. So, the 95% CI of \(x\) is [-1.96, 1.96].
Under the assumption of MLR.1 through MLR.6 (which includes the normality assumption of the error), we learned that
\(\frac{\widehat{\beta}_j - \beta_j}{\widehat{se(\widehat{\beta}_j)}} \sim t_{n-k-1}\)
So, following the general procedure we discussed in the previous slide, the A% confidence interval of \(\frac{\widehat{\beta}_j - \beta_j}{\widehat{se(\widehat{\beta}_j)}}\) is
- lower bound: \((100 − A)/2\)% quantile of the \(t_{n-k-1}\) distribution (let’s call this \(Q_l\))
- upper bound: \(100 - (100 − A)/2\)% quantile of the \(t_{n-k-1}\) distribution (let’s call this \(Q_h\))
But, we want the A% CI of \(\beta_j\), not \(\frac{\widehat{\beta}_j - \beta_j}{\widehat{se(\widehat{\beta}_j)}}\). Solving for \(\beta_j\),
\(\beta_j = t_{n-k-1}\times \widehat{se(\widehat{\beta}_j)} + \widehat{\beta}_j\)
So, to get the A% CI of \(\beta_j\), we scale the CI of \(\frac{\widehat{\beta}_j - \beta_j}{\widehat{se(\widehat{\beta}_j)}}\) by \(se(\widehat{\beta}_j)\) and then shift by \(\widehat{\beta}_j\).
- lower bound: \(Q_l \times se(\widehat{\beta}_j) + \widehat{\beta}_j\)
- upper bound: \(Q_h \times se(\widehat{\beta}_j) + \widehat{\beta}_j\)
Note that \(Q_l\) is negative and \(Q_h\) is negative.
Run OLS and extract necessary information
Applying broom::tidy() to wage_reg,
We are interested in getting the 90% confidence interval of the coefficient on educ \((\beta_{educ})\). Under all the assumptions (MLR.1 through MLR.6), we know that in general,
\(\frac{\widehat{\beta}_{educ} - \beta_{educ}}{\widehat{se(\widehat{\beta}_{educ})}} \sim t_{n-k-1}\)
Specifically for this regression,
\(\widehat{\beta}_{educ}\) = 0.5989651
\(\widehat{se(\widehat{\beta}_{educ})}\) = 0.0512835
\(n - k - 1 = 490\) (degrees of freedom)
Now, we need to find the 5% ((100-90)/2) and 95% (100-(100-90)/2) quantile of \(t_{522}\).
So, the 90% CI of \(\frac{0.599 - \beta_{educ}}{0.051} \sim t_{522}\) is [-1.6477779, 1.6477779]
By scaling and shifting, the lower and upper bounds of the 90% CI of \(\beta_{educ}\) are:
lower bound: 0.599 + 0.051 \(\times\) -1.6477779 = 0.5149633
upper bound: 0.599 + 0.051 \(\times\) 1.6477779 = 0.6830367
The distribution of \(t_{522}\):
You can just use broom::tidy() with conf.int = TRUE, conf.level = confidence level like below:
Linear Combination of Multiple Coefficients
Linear Combination of Multiple Coefficients
- Example
- Rewrite the hypothesis
- Math
- Going back to the example
- get \(se(\widehat{\beta}_1-\widehat{\beta}_2)\)
- Demonstration using R
Model
\[log(wage) = \beta_0+\beta_1 jc+ \beta_2 univ + \beta_3 exper + u\]
- \(jc\): 1 if you attended 2-year college, 0 otherwise
- \(univ\): 1 if you attended 4-year college, 0 otherwise
Question
Does the impact of education on wage is greater if you attend a 4-year college than 2-year college?
Hypothesis
The null and alternative hypotheses would be:
- \(H_1:\) \(\beta_1 < \beta_2\)
- \(H_0:\) \(\beta_1 = \beta_2\)
The null and alternative hypotheses are:
- \(H_1:\) \(\beta_1 < \beta_2\)
- \(H_0:\) \(\beta_1 = \beta_2\)
Rewriting them,
- \(H_1:\) \(\beta_1-\beta_2 < 0\)
- \(H_0:\) \(\beta_1 - \beta_2 =0\)
Or,
- \(H_1:\) \(\alpha < 0\)
- \(H_0:\) \(\alpha =0\)
where \(\alpha = \beta_1 - \beta_2\)
Note that \(\alpha\) is a linear combination of \(\beta_1\) and \(\beta_2\).
Important Fact
For any linear combination of the OLS coefficients, denoted as \(\widehat{\alpha}\), the following holds:
\[\frac{\widehat{\alpha}-\alpha}{\widehat{se(\widehat{\alpha})}} \sim t_{n-k-1}\]
Where \(\alpha\) is the true value (it is \(\beta_1 - \beta_2\) in the example in the previous slide).
So, using the example, this means that
\[\frac{\widehat{\alpha}-\alpha}{\widehat{se(\widehat{\alpha})}} = \frac{\widehat{\beta}_1-\widehat{\beta}_2-(\beta_1 - \beta_2)}{\widehat{se(\widehat{\beta}_1-\widehat{\beta}_2)}} \sim t_{n-k-1}\]
This is great because we know how to do t-test!
Our null hypothesis is \(\alpha = 0\) (or \(\beta_1 - \beta_2 = 0\)).
So, If indeed the null hypothesis is true, then
\[\frac{\widehat{\alpha}-0}{\widehat{se(\widehat{\alpha})}} = \frac{\widehat{\beta}_1-\widehat{\beta}_2-0}{\widehat{se(\widehat{\beta}_1-\widehat{\beta}_2)}} \sim t_{n-k-1}\]
So, all you need to do is to substitute \(\widehat{\beta}_1\), \(\widehat{\beta}_2\), \(\widehat{se(\widehat{\beta}_1 - \widehat{\beta}_2)}\) into the formula and see if the value is beyond the critical value for your chosen level of statistical significance.
But,
\[se(\widehat{\beta}_1-\widehat{\beta}_2)= \sqrt{Var(\widehat{\beta}_1-\widehat{\beta}_2}) \ne \sqrt{Var(\widehat{\beta}_1)+Var(\widehat{\beta}_2)}\]
If the following was true,
\[se(\widehat{\beta}_1-\widehat{\beta}_2) = \sqrt{Var(\widehat{\beta}_1)+Var(\widehat{\beta}_2)}\]
then, we could have just extracted \(Var(\widehat{\beta}_1)\) and \(Var(\widehat{\beta}_2)\) individually from the regression object on R, sum them up, and take a square root of it.
Math aside
\[Var(ax+by) = a^2 Var(x) + 2abCov(x,y) + b^2 Var(y)\]
So,
\[se(\widehat{\beta}_1-\widehat{\beta}_2)= \sqrt{Var(\widehat{\beta}_1-\widehat{\beta}_2}) = \sqrt{Var(\widehat{\beta}_1)-2Cov(\widehat{\beta}_1,\widehat{\beta}_2)+Var(\widehat{\beta}_2)}\]
Definition
Variance covariance matrix is a matrix where
- \(VCOV_{i,i}\): the variance of \(i\)th variable’s coefficient estimator
- \(VCOV_{i,j}\): the covariance between \(i\)th and \(j\)th variables’ estimators
You can get it by applying vcov() to regression results:
For example, \(vcov_{sc}[2, 2]\) is the variance of \(\widehat{\beta}_{jc}\), and \(vcov_{sc}[2, 3]\) is the covariance between \(\widehat{\beta}_{jc}\) and \(\widehat{\beta}_{univ}\).
Get coefficient estimates:
Calcualt t-statistic:
In practice, you can just use car::linearHypothesis() to implement t-test involving a linear combination of multiple coefficients.
Syntax
Example
Please note that it runs \(\chi^2\) test. When t-statistic is squared, it follows a \(\chi^2\) distribution. So, it calcualtes the square of the t-statistic and look up the \(\chi^2\) distribution critical value to decide whether to reject the null or not.
Let’s confirm this:
Yes, this is the same as the \(\chi^2\) value reported by car::linearHypothesis(reg_sc, "jc=univ")
Important
The test results would be the same whether you run t-test or \(\chi^2\) test.
Multiple Linear Restrictions: F-test
Multiple Linear Restrictions: F-test
Model
\[log(salary) = \beta_0 + \beta_1 years + \beta_2 gamesyr + \beta_3 bavg + \beta_4 hrunsyr + \beta_5 rbisyr + u\]
- \(salary\): salary in 1993
- \(years\): years in the league
- \(gamesyr\): average games played per year
- \(bavg\): career batting average
- \(hrunsyr\): home runs per year
- \(rbisyr\): runs batted in per year
Hypothesis
Once years in the league and games per year have been controlled for, the statistics measuring performance ( \(bavg\), \(hrunsyr\), \(rbisyr\)) have no effect on salary collectively.
\(H_0\): \(\beta_3=0\), \(\beta_4=0\), and \(\beta_5=0\)
\(H_1\): \(H_0\) is not true
How do we test this?
- \(H_0\) holds if all of \(\beta_3\), \(\beta_4\), or \(\beta_5\) are zero.
- Conduct t-test for each coefficient individually?
What do you find?
None of the coefficients on bavg, hrunsyr, and rbisyr is statistically significantly different from 0 even at the 10% level!!
So, does this mean that they collectively have no impact on the salary of MLB players?
If you were to conclude that they do not have statistically significant impact jointly, you would turn out to be wrong!!
\(SSR\) (or \(R^2\)) turns out to be useful for testing their impacts jointly.
In doing an F-test of the null hypothesis, we compare sum of squared residuals \((SSR)\) of two models:
Unrestricted Model
\[log(salary) = \beta_0 + \beta_1 years + \beta_2 gamesyr + \beta_3 bavg + \beta_4 hrunsyr + \beta_5 rbisyr + u\]
Restricted Model
\[log(salary) = \beta_0 + \beta_1 years + \beta_2 gamesyr + u\]
The coefficients on \(bavg\), \(hrunsyr\), and \(rbisyr\) are restricted to be 0 following the null hypothesis.
If the null hypothesis is indeed true, then what do you think is going to happen if you compare the \(SSR\) of the two models? Which one has a bigger \(SSR\)?
\(SSR\) from the restricted model should be large because the restricted model has a smaller explanatory power than the unrestricted model.
SSR of the unrestricted model: \(SSR_u\)
SSR of the restricted model: \(SSR_r\)
What does \(SSR_r - SSR_u\) measure?
The contribution from the three excluded variables in explaining the dependent variable.
Is the contribution large enough to say that the excluded variables are important?
Cannot tell at this point because we do not know the distribution of the difference!
Setup
Consider a following general model:
\[ y = \beta_0 +\beta_1 x_1 + \dots+\beta_k x_k +u \]
Suppose we have \(q\) restrictions to test: that is, the null hypothesis states that \(q\) of the variables have zero coefficients.
\[H_0: \beta_{k-q+1} =0, \beta_{k-q+2} =0, \dots, \beta_k=0\]
When we impose the restrictions under \(H_0\), the restricted model is the following:
\[y = \beta_0 +\beta_1 x_1 + \dots+\beta_{k-q} x_{k-q} + u\]
F-statistic
If the null hypothesis is true, then,
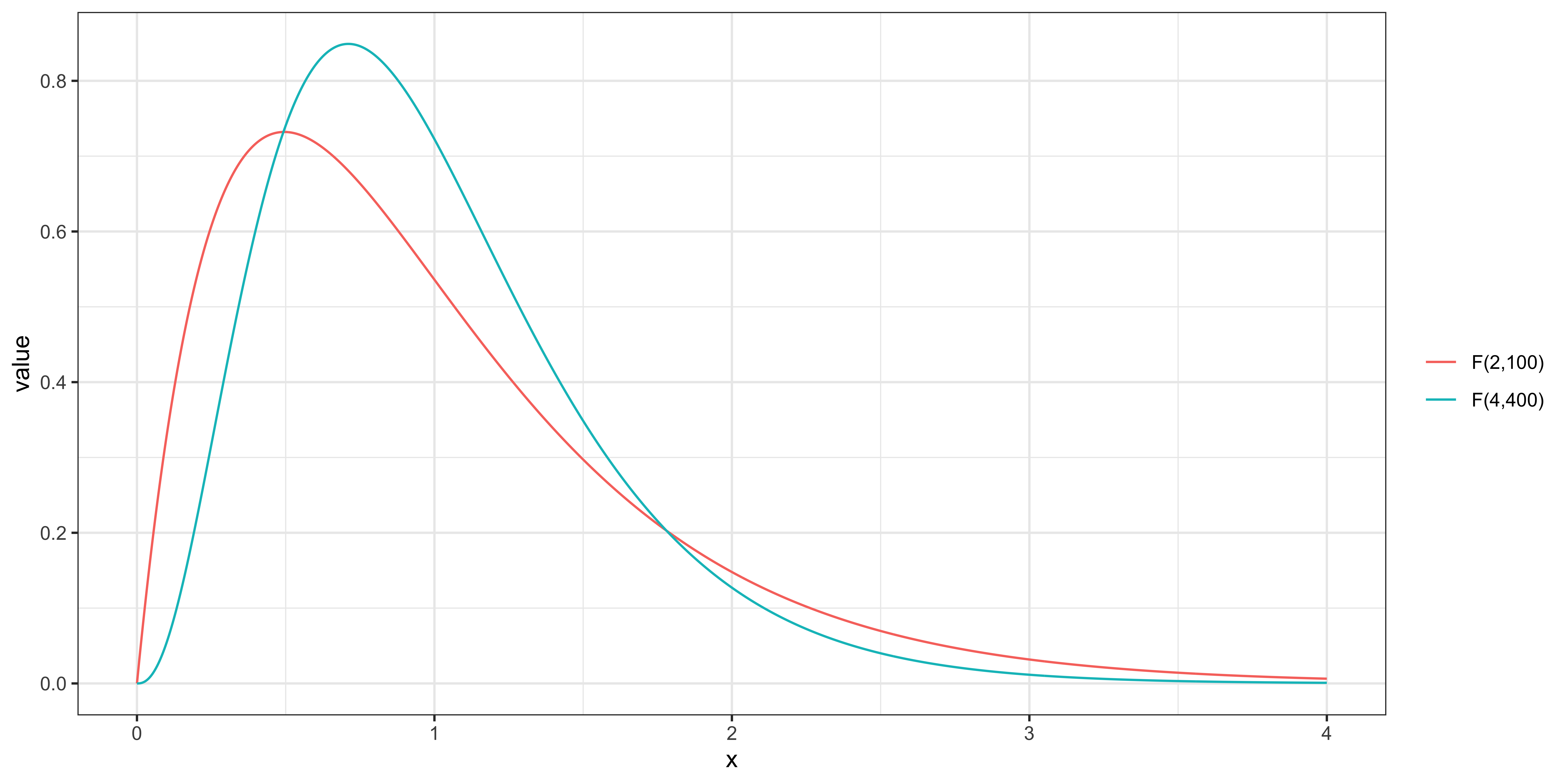
\[F = \frac{(SSR_r-SSR_u)/q}{SSR_u/(n-k-1)} \sim F_{q,n-k-1}\]
- \(q\): the number of restrictions
- \(n-k-1\): degrees of freedom of residuals
Is the above \(F\)-statistic always positive?
Yes, because \(SSR_r-SSR_u\) is always positive.
The greater the joint contribution of the \(q\) variables, the (greater or smaller) the \(F\)-statistic?
Greater.
F-distribution
F-test steps
- Define the null hypothesis
- Estimate the unrestricted and restricted models to obtains their \(SSR\)
- Calculate \(F\)-statistic
- Define the significance level and corresponding critical value according to the F distribution with appropriate degrees of freedoms
- Reject if your \(F\)-statistic is greater than the critical value, otherwise do not reject
Eestimate the unrestricted and restricted models
Calculate F-stat
Find the critical value
Is F-stat > critical value?
Observation
So, the performance variables have statistically significant impacts on salary jointly!!
What happened?
You can use the car::linearHypothesis() function from the car package.
Syntax
regression: the name of the regression results of the unrestricted modelhypothesis” text of null hypothesis. For example,
c("x1 = 0", "x2 = 1") means the coefficients on \(x1\) and \(x2\) are \(0\) and \(1\), respectively
The following code test if \(\beta_{bavg} = 0\), \(\beta_{hrunsyr} = 0\), and \(\beta_{rbisyr} = 0\).
Simulation (multicollinearity, t-test, and F-test)
x1 and x2 are highly correlated with each other:
Both x1 and x2 are statistically insignificant individually.
The F-statistic for the hypothesis testing is:
The F-statistic is very high, meaning they collectively affect the dependent variable significantly.
The standard error estimates of the coefficients on x1 and x2 are very high because they are so highly correlated that your estimation of the model had such a difficult time to distinguish the their individual impacts.
But, collectively, they have large impacts. \(F\)-test was able to detect the statistical significance of their impacts collectively.
MLB example
Here is the correlation coefficients between the three variables:
As you can see, brunsyr and hrunsyr are highly correlated with each other.
They are not so highly correlated with bavg.
The test of a linear combination of the parameters we looked at earlier is a special case of F-test where the number of restriction is 1.
It can be shown that square root of \(F_{1, df}\) follows the \(t_{df}\) distribution.
So, we can actually use \(F\)-test for this type of hypothesis testing because \(F_{1,t-n-k} \sim t_{t-n-k}^2\).
Check with the previous slide of the same t-test and confirm that the t-statistics we got there and here are the same.