00: Introduction to Econometrics

What is econometrics about?

What econometrics is about

What are we doing?

Estimate quantitative relationships between variables.


Examples

  • the impact of fertilizer on crop yield
  • the impact of political campaign expenditure on voting outcomes
  • the impact of education on wage
  1. formulation of the question of interest (what are you trying to find out?)
  2. develop an economic model of the phenomenon you are interested in understanding (identify variables that matter)
  3. turn the economic model into an econometric model
  4. collect data
  5. estimate the model using econometrics
  6. test hypotheses

Go through the steps

Example: Job training and worker productivity

\[wage = f(educ,exper,training)\]

  • \(wage\): hourly wage
  • \(educ\): years of formal education
  • \(exper\): years of workforce experience
  • \(training\): weeks spent in job training

Note

Depending on questions you would like to answer, the economic model can (and should) be much more involved

We have built a conceptual model:

\[wage = f(educ,exper,training)\]

Now, the form of the function \(f(\cdot)\) must be specified (almost always) before we can undertake an econometric analysis

\[ wage = \beta_0 + \beta_1 educ + \beta_2 exper + \beta_3 training + u \]

\(\beta_0,\beta_1,\beta_2,\beta_3\)

  • are the parameters of the econometric model.
  • describe the directions and strengths of the relationship between \(wage\) and the factors used to determine \(wage\) in the model

\(u\)

  • is called error term
  • includes ALL the other factors that can affect wage other than the included variables (like innate ability)

We can collect data using various ways. Some of them include survey, websites, experiments. Let’s look at different data types:

  • Sample of individuals, households, firms, cities, states, countries, or a variety of other units, taken at a given point in time
  • The data on all units do not correspond to precisely the same time period
    • some families surveyed during different weeks within a year

What a cross-sectional data looks like on R

      wage  educ exper female married
     <num> <int> <int>  <int>   <int>
  1:  3.10    11     2      1       0
  2:  3.24    12    22      1       1
  3:  3.00    11     2      0       0
  4:  6.00     8    44      0       1
  5:  5.30    12     7      0       1
 ---                                 
522: 15.00    16    14      1       1
523:  2.27    10     2      1       0
524:  4.67    15    13      0       1
525: 11.56    16     5      0       1
526:  3.50    14     5      1       0

Observations on a variable or several variables over time + corn price + oil price


Note

  • The econometric frameworks necessary to analyze time series data are quite different from those for cross-sectional data
  • We do NOT learn time-series econometric methods

Time series data for each cross-sectional member in the data set ( same cross-sectional units are tracked over a given period of time)

Example

  • wage data for individuals collected every five years over the past 30 years
  • yearly GDP data for 60 countries over the past 10 years

What a panel data looks like on R

     county  year    crmrte   prbarr  prbpris
      <int> <int>     <num>    <num>    <num>
  1:      1    81 0.0398849 0.289696 0.472222
  2:      1    82 0.0383449 0.338111 0.506993
  3:      1    83 0.0303048 0.330449 0.479705
  4:      1    84 0.0347259 0.362525 0.520104
  5:      1    85 0.0365730 0.325395 0.497059
 ---                                         
626:    197    83 0.0155747 0.226667 0.428571
627:    197    84 0.0136619 0.204188 0.372727
628:    197    85 0.0130857 0.180556 0.333333
629:    197    86 0.0128740 0.112676 0.244444
630:    197    87 0.0141928 0.207595 0.360825

This is what you learn for the next few months!!

  • estimate the model using econometrics
  • test hypothesis

Causality and Association

Causality and Association

Association

An association of two variables arise because either of or both variables affect the other variable

\[\begin{align} A \longleftrightarrow B \\ A \longrightarrow B \\ A \longleftarrow B \end{align}\]

Association does NOT concern which affects which. Under all the three cases above, A and B are associated. Or, we say there is an association between A and B. This is what correlation coefficient measures.


Causality

When A has a causal impact on B,

\[ A \longrightarrow B \]

Here, changes in \(A\) cause changes in \(B\), not the other way around

Let’s watch this interesting CM.

People who wear glasses are

  • much smarter than those who don’t
  • more likely to pursue higher education
  • 200% more likely to graduate college

For you to be convinced to buy glasses, these claims needs to be causal, not association:

  • Does wearing glasses make you much smarter?
  • Does wearing glasses make it more likely for you to pursue higher education?
  • Does wearing glasses make it 200% more likely for you to graduate college?

However, this seems to be a more likely explanation of the association:

  • One spends more time studying academic subjects
    • smarter (or knowledgeable) \(\Rightarrow\) pursue higher education and graduate college
    • worsened eyesight \(\Rightarrow\) wear glasses

Important

  • We care about isolating causal effects, but not association
  • Identifying association is super easy
  • Identifying causal effects is extremely hard (this is what we tackle)

Endogeneity: Your Nemesis

Endogeneity: Your Nemesis

It is super easy to find an association of multiple variables, but it is incredibly hard to find a causal effect (at least in Economics)!!

That is due to the problem called endogeneity , which is going to be defined formally later.

You are interested in the causal impact of fire fighters on the number of death tolls in fire events

fire event

death toll

# of firefighters deployed

1

10

20

2

0

3

3

5

10

4

3

5

5

50

50

Questions

  • How are they associated ?
  • Can you say anything about the causal effect of fire fighters deployment on the number of death tolls?

You ignored an important variable!!

fire event

death toll

# of firefighters deployed

scale of fire

1

10

20

20

2

0

3

5

3

5

10

20

4

3

5

10

5

50

50

100

Definition

Variables of interest are correlated with some unobservables (variables that cannot be observed or are missing) that have non-zero impacts on the variable that you want to explain


The unobserved variables are also called confounder/confounding factor .

The example

In the the firefighter example,

  • variable of interest : the number of firefighters
  • unobservables/confounder : the scale of fire events (and other factors)
  • variable to explain : death toll

The model

\[\begin{align} \mbox{death toll} & = \alpha + \beta\; \mbox{# of fire fighters} + \mu\\ ,\mbox{where } \mu & = (\gamma\; \mbox{scale} + v) \mbox{ is the error term (collection of unobservables)} \end{align}\]

Endogeneity Problem

# of fire fighters is correlated with scale, which we ignored

\[wage = \beta_0 + \beta_1 educ + \beta_2 exper + \beta_3 training + u\]

What are unobservables in \(u\) that are likely to be correlated with \(educ\)?

An important unobservable

  • innate ability \(\Rightarrow\) wage
  • innate ability \(\Rightarrow\) education

How to deal with endogeneity

Problem

Most of the time, you will be faced with endogeneity problems caused by at least one of the followings,

  • omitted variables (the scale of fire events, innate ability)
  • self-selection
  • simultaneity
  • measurement error

Central Question

How can we avoid or solve endogeneity problems?

  • You have two opportunities to deal with endogeneity problems
    • at the design (design to collect data) stage
    • at the regression stage (what you will learn in this course)
  • Econometrics has evolved mostly to address endogeneity problems at the regression stage because randomized experiments are infeasible most of the time
  • How about econometrics and other fields of statistics: Statistics, Psychometrics, and Biometrics?

Field

Design

Estimation Method

Econometrics

not feasible (often)

intricate

Many other fields

feasible

relatively simple

Randomized-experiments

In randomized experiments,

  • you have a liberty to determine the level of the variable of interest
  • by randomizing the value of the variable of interest, you can effectively break the link (association) with whatever is included in the error term

Yield and nitrogen rate data obtained from a field that is managed by a farmer

Farmer

  • decide nitrogen rate based on soil/field characteristics (some of them we researchers do not get to observe)

Researcher

  • soil characteristics is not observable, so it is in the error term

\[yield = \beta_0 + \beta_1 N + (\gamma SC + \mu)\]

  • N (nitrogen rate) and SC (soil characteristics) are correlated

Suppose the farmer applied more nitrogen to the area where its soil characteristics lead to higher corn yield

Question If the researcher estimate the model (which ignores soil characteristics), do you over- or under-estimate the impact of nitrogen rate on corn yield?

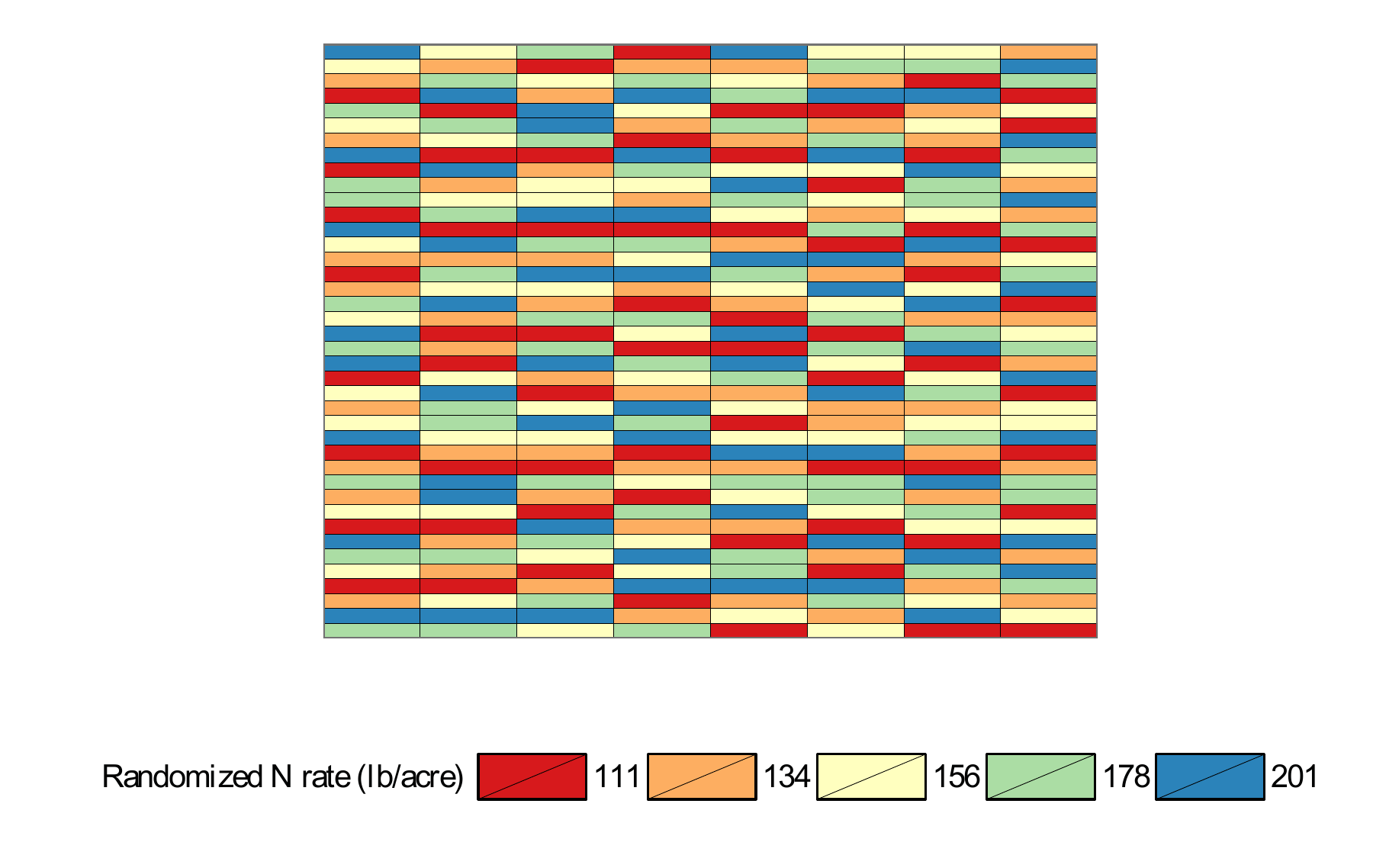
Important

Soil quality (in error term) is no longer correlated with N!!

Randomized Experiment?

Researchers determine randomly how much education subjects (people) can get?

Endogeneity Problem in Economics

  • Economics is about understanding human behavior

  • Almost always, you need to deal with endogeneity problem because people are smart: we make decisions based on available information (not just randomly) so that our decisions lead to good outcomes (whether our decisions turn out to be good or not is irrelevant)

    • how much education one get is determined based on their judgment of their own ability (not by rolling a dice)
    • how many fire fighters to be deployed was determined based on the scale of fire (not by rolling a dice)
    • how much nitrogen to apply based on soil characteristics (not by rolling a dice)

  • If people are not smart and just roll a dice for their decision making, we would have much easier time identifying causal effects